• Home
• com.github.javadev
• leetcode-in-java
• 1.17
• source code
• readme.md

×

Project download

Many resources are needed to download a project. Please understand that we have to compensate our server costs. Thank you in advance.
Project price only 1 $

You can buy this project and download/modify it how often you want.

g1701_1800.s1765_map_of_highest_peak.readme.md Maven / Gradle / Ivy

1765\. Map of Highest Peak

Medium

You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.

*   If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
*   If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.

You must assign each cell a height in a way that follows these rules:

*   The height of each cell must be non-negative.
*   If the cell is a **water** cell, its height must be `0`.
*   Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

Find an assignment of heights such that the maximum height in the matrix is **maximized**.

Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.

**Example 1:**

**![](https://assets.leetcode.com/uploads/2021/01/10/screenshot-2021-01-11-at-82045-am.png)**

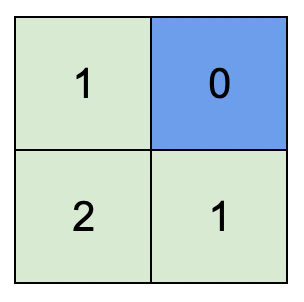**Input:** isWater = [[0,1],[0,0]]

**Output:** [[1,0],[2,1]]

**Explanation:** The image shows the assigned heights of each cell. The blue cell is the water cell, and the green cells are the land cells.

**Example 2:**

**![](https://assets.leetcode.com/uploads/2021/01/10/screenshot-2021-01-11-at-82050-am.png)**

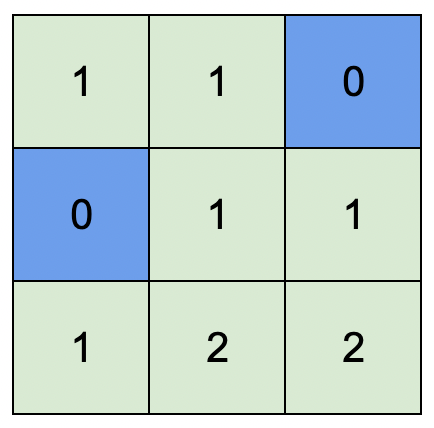**Input:** isWater = [[0,0,1],[1,0,0],[0,0,0]]

**Output:** [[1,1,0],[0,1,1],[1,2,2]]

**Explanation:** A height of 2 is the maximum possible height of any assignment. Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.

**Constraints:**

*   `m == isWater.length`
*   `n == isWater[i].length`
*   `1 <= m, n <= 1000`
*   `isWater[i][j]` is `0` or `1`.
*   There is at least **one** water cell.