• Home
• com.github.javadev
• leetcode-in-java
• 1.7
• source code
• readme.md

×

Project download

Many resources are needed to download a project. Please understand that we have to compensate our server costs. Thank you in advance.
Project price only 1 $

You can buy this project and download/modify it how often you want.

g0901_1000.s0980_unique_paths_iii.readme.md Maven / Gradle / Ivy

980\. Unique Paths III

Hard

You are given an `m x n` integer array `grid` where `grid[i][j]` could be:

*   `1` representing the starting square. There is exactly one starting square.
*   `2` representing the ending square. There is exactly one ending square.
*   `0` representing empty squares we can walk over.
*   `-1` representing obstacles that we cannot walk over.

Return _the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once_.

**Example 1:**

![](https://assets.leetcode.com/uploads/2021/08/02/lc-unique1.jpg)

**Input:** grid = [[1,0,0,0],[0,0,0,0],[0,0,2,-1]]

**Output:** 2

**Explanation:** We have the following two paths:

1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)

2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

**Example 2:**

![](https://assets.leetcode.com/uploads/2021/08/02/lc-unique2.jpg)

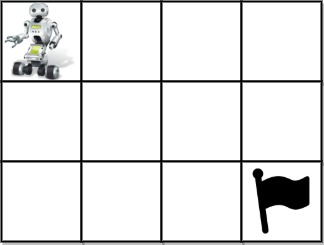
**Input:** grid = [[1,0,0,0],[0,0,0,0],[0,0,0,2]]

**Output:** 4

**Explanation:** We have the following four paths:

1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)

2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)

3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)

4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

**Example 3:**

![](https://assets.leetcode.com/uploads/2021/08/02/lc-unique3-.jpg)

**Input:** grid = [[0,1],[2,0]]

**Output:** 0

**Explanation:** There is no path that walks over every empty square exactly once.

Note that the starting and ending square can be anywhere in the grid.

**Constraints:**

*   `m == grid.length`
*   `n == grid[i].length`
*   `1 <= m, n <= 20`
*   `1 <= m * n <= 20`
*   `-1 <= grid[i][j] <= 2`
*   There is exactly one starting cell and one ending cell.