g0001_0100.s0074_search_a_2d_matrix.readme.md Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
The newest version!
74\. Search a 2D Matrix

Medium

Write an efficient algorithm that searches for a value in an `m x n` matrix. This matrix has the following properties:

*   Integers in each row are sorted from left to right.
*   The first integer of each row is greater than the last integer of the previous row.

**Example 1:**

![](https://assets.leetcode.com/uploads/2020/10/05/mat.jpg)

**Input:** matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3

**Output:** true 

**Example 2:**

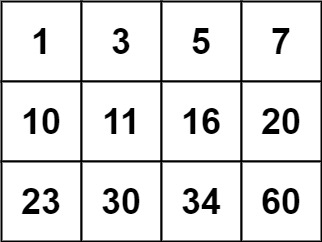
![](https://assets.leetcode.com/uploads/2020/10/05/mat2.jpg)

**Input:** matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13

**Output:** false 

**Constraints:**

*   `m == matrix.length`
*   `n == matrix[i].length`
*   `1 <= m, n <= 100`
*   -10⁴ <= matrix[i][j], target <= 10⁴

To solve the "Search a 2D Matrix" problem in Java with the Solution class, follow these steps:

1. Define a method `searchMatrix` in the `Solution` class that takes a 2D integer matrix `matrix` and an integer `target` as input and returns `true` if the target value is found in the matrix, otherwise returns `false`.
2. Initialize two pointers `row` and `col` to start at the top-right corner of the matrix. `row` starts from 0 and `col` starts from the last column.
3. Loop until `row` is less than the number of rows in the matrix and `col` is greater than or equal to 0:
   - If `matrix[row][col]` is equal to the target, return `true`.
   - If `matrix[row][col]` is greater than the target, decrement `col`.
   - If `matrix[row][col]` is less than the target, increment `row`.
4. If the target is not found after the loop, return `false`.

Here's the implementation of the `searchMatrix` method in Java:

```java
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        
        int row = 0;
        int col = n - 1;
        
        while (row < m && col >= 0) {
            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] > target) {
                col--;
            } else {
                row++;
            }
        }
        
        return false;
    }
}
```

This implementation searches for the target value efficiently in the given matrix by starting from the top-right corner and moving either left or down based on the comparison with the target value. The time complexity of this solution is O(m + n), where m is the number of rows and n is the number of columns in the matrix.