g0101_0200.s0124_binary_tree_maximum_path_sum.readme.md Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
The newest version!
124\. Binary Tree Maximum Path Sum

Hard

A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.

The **path sum** of a path is the sum of the node's values in the path.

Given the `root` of a binary tree, return _the maximum **path sum** of any **non-empty** path_.

**Example 1:**

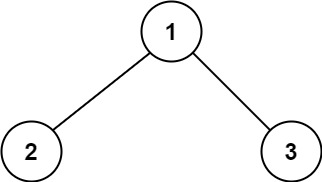
![](https://assets.leetcode.com/uploads/2020/10/13/exx1.jpg)

**Input:** root = [1,2,3]

**Output:** 6

**Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6. 

**Example 2:**

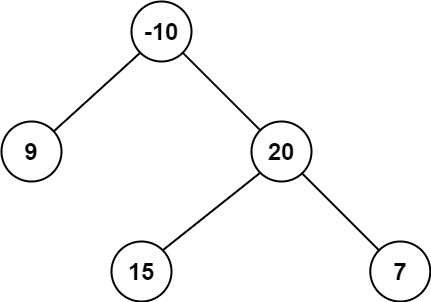
![](https://assets.leetcode.com/uploads/2020/10/13/exx2.jpg)

**Input:** root = [-10,9,20,null,null,15,7]

**Output:** 42

**Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42. 

**Constraints:**

*   The number of nodes in the tree is in the range [1, 3 * 10⁴].
*   `-1000 <= Node.val <= 1000`

To solve the "Binary Tree Maximum Path Sum" problem in Java with a `Solution` class, we'll use a recursive approach. Below are the steps:

1. **Create a `Solution` class**: Define a class named `Solution` to encapsulate our solution methods.

2. **Create a `maxPathSum` method**: This method takes the root node of the binary tree as input and returns the maximum path sum.

3. **Define a recursive helper method**: Define a recursive helper method `maxSumPath` to compute the maximum path sum rooted at the current node.
   - The method should return the maximum path sum that can be obtained from the current node to any of its descendants.
   - We'll use a post-order traversal to traverse the tree.
   - For each node:
     - Compute the maximum path sum for the left and right subtrees recursively.
     - Update the maximum path sum by considering three cases:
       1. The current node itself.
       2. The current node plus the maximum path sum of the left subtree.
       3. The current node plus the maximum path sum of the right subtree.
     - Update the global maximum path sum if necessary by considering the sum of the current node, left subtree, and right subtree.

4. **Initialize a variable to store the maximum path sum**: Initialize a global variable `maxSum` to store the maximum path sum.

5. **Call the helper method**: Call the `maxSumPath` method with the root node.

6. **Return the maximum path sum**: After traversing the entire tree, return the `maxSum`.

Here's the Java implementation:

```java
class Solution {
    int maxSum = Integer.MIN_VALUE; // Initialize global variable to store maximum path sum
    
    public int maxPathSum(TreeNode root) {
        maxSumPath(root);
        return maxSum; // Return maximum path sum
    }
    
    // Recursive helper method to compute maximum path sum rooted at current node
    private int maxSumPath(TreeNode node) {
        if (node == null) return 0; // Base case
        
        // Compute maximum path sum for left and right subtrees recursively
        int leftSum = Math.max(maxSumPath(node.left), 0); // Ignore negative sums
        int rightSum = Math.max(maxSumPath(node.right), 0); // Ignore negative sums
        
        // Update maximum path sum by considering three cases:
        // 1. Current node itself
        // 2. Current node + maximum path sum of left subtree
        // 3. Current node + maximum path sum of right subtree
        int currentSum = node.val + leftSum + rightSum;
        maxSum = Math.max(maxSum, currentSum); // Update global maximum path sum
        
        // Return the maximum path sum that can be obtained from the current node to any of its descendants
        return node.val + Math.max(leftSum, rightSum);
    }
    
    // Definition for a binary tree node
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        
        TreeNode() {}
        TreeNode(int val) { this.val = val; }
        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }
}
```

This implementation follows the steps outlined above and efficiently computes the maximum path sum in a binary tree in Java.