g0701_0800.s0785_is_graph_bipartite.readme.md Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

The newest version!

785\. Is Graph Bipartite?

Medium

There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:

*   There are no self-edges (`graph[u]` does not contain `u`).
*   There are no parallel edges (`graph[u]` does not contain duplicate values).
*   If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
*   The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.

A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.

Return `true` _if and only if it is **bipartite**_.

**Example 1:**

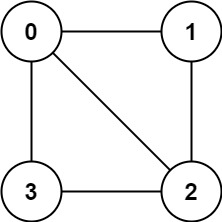
![](https://assets.leetcode.com/uploads/2020/10/21/bi2.jpg)

**Input:** graph = [[1,2,3],[0,2],[0,1,3],[0,2]]

**Output:** false

**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

**Example 2:**

![](https://assets.leetcode.com/uploads/2020/10/21/bi1.jpg)

**Input:** graph = [[1,3],[0,2],[1,3],[0,2]]

**Output:** true

**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.

**Constraints:**

*   `graph.length == n`
*   `1 <= n <= 100`
*   `0 <= graph[u].length < n`
*   `0 <= graph[u][i] <= n - 1`
*   `graph[u]` does not contain `u`.
*   All the values of `graph[u]` are **unique**.
*   If `graph[u]` contains `v`, then `graph[v]` contains `u`.