• Home
• com.github.javadev
• leetcode-in-java
• 1.38
• source code
• readme.md

×

Project download

Many resources are needed to download a project. Please understand that we have to compensate our server costs. Thank you in advance.
Project price only 1 $

You can buy this project and download/modify it how often you want.

g2101_2200.s2103_rings_and_rods.readme.md Maven / Gradle / Ivy

2103\. Rings and Rods

Easy

There are `n` rings and each ring is either red, green, or blue. The rings are distributed **across ten rods** labeled from `0` to `9`.

You are given a string `rings` of length `2n` that describes the `n` rings that are placed onto the rods. Every two characters in `rings` forms a **color-position pair** that is used to describe each ring where:

*   The **first** character of the ith pair denotes the ith ring's **color** (`'R'`, `'G'`, `'B'`).
*   The **second** character of the ith pair denotes the **rod** that the ith ring is placed on (`'0'` to `'9'`).

For example, `"R3G2B1"` describes `n == 3` rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.

Return _the number of rods that have **all three colors** of rings on them._

**Example 1:**

![](https://assets.leetcode.com/uploads/2021/11/23/ex1final.png)

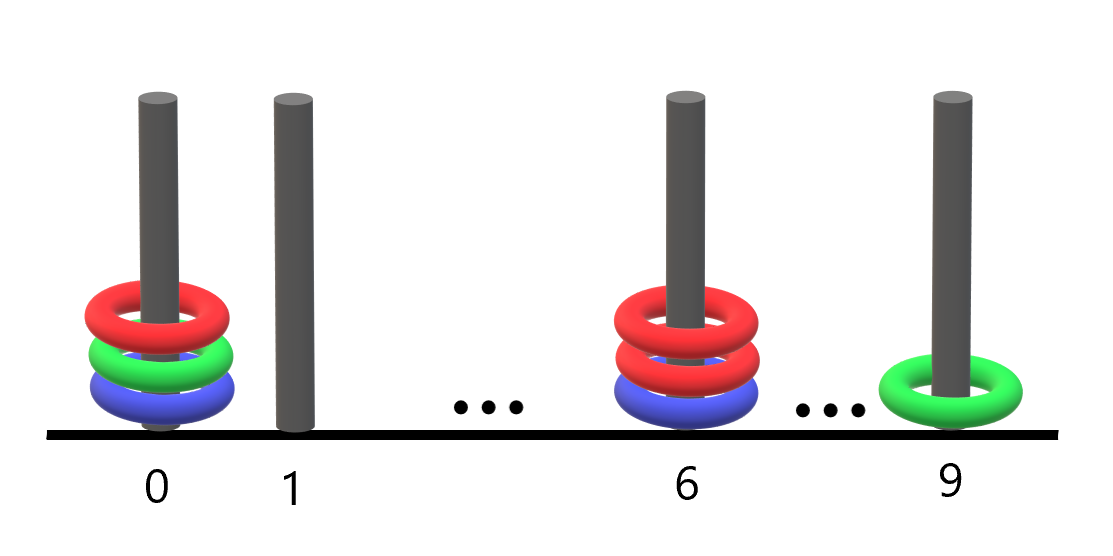
**Input:** rings = "B0B6G0R6R0R6G9"

**Output:** 1

**Explanation:** 

- The rod labeled 0 holds 3 rings with all colors: red, green, and blue. 

- The rod labeled 6 holds 3 rings, but it only has red and blue. 

- The rod labeled 9 holds only a green ring. 
  
Thus, the number of rods with all three colors is 1.

**Example 2:**

![](https://assets.leetcode.com/uploads/2021/11/23/ex2final.png)

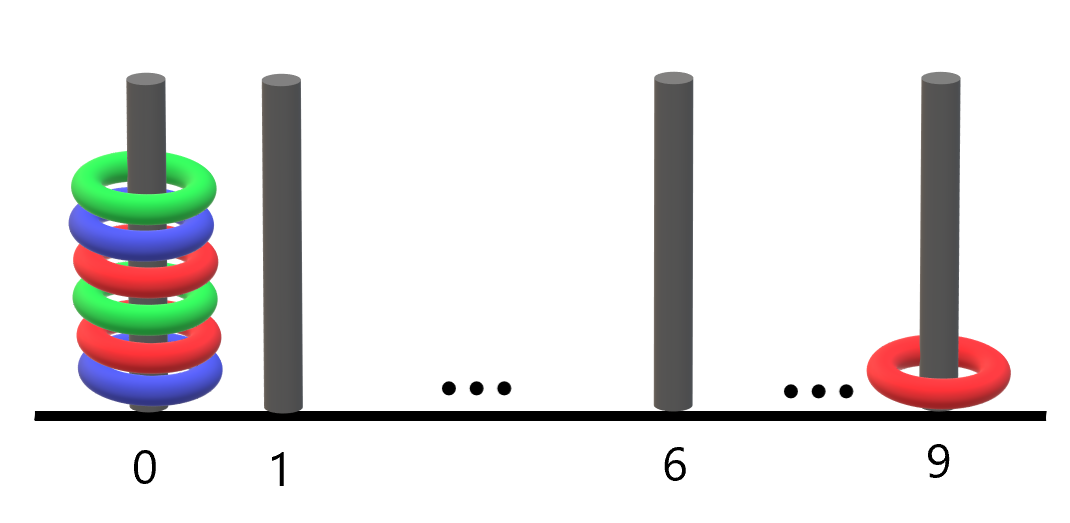
**Input:** rings = "B0R0G0R9R0B0G0"

**Output:** 1

**Explanation:** 

- The rod labeled 0 holds 6 rings with all colors: red, green, and blue. 

- The rod labeled 9 holds only a red ring. 
  
Thus, the number of rods with all three colors is 1.

**Example 3:**

**Input:** rings = "G4"

**Output:** 0

**Explanation:** Only one ring is given. Thus, no rods have all three colors.

**Constraints:**

*   `rings.length == 2 * n`
*   `1 <= n <= 100`
*   `rings[i]` where `i` is **even** is either `'R'`, `'G'`, or `'B'` (**0-indexed**).
*   `rings[i]` where `i` is **odd** is a digit from `'0'` to `'9'` (**0-indexed**).