• Home
• com.github.javadev
• leetcode-in-java
• 1.38
• source code
• readme.md

×

Project download

Many resources are needed to download a project. Please understand that we have to compensate our server costs. Thank you in advance.
Project price only 1 $

You can buy this project and download/modify it how often you want.

g3201_3300.s3242_design_neighbor_sum_service.readme.md Maven / Gradle / Ivy

3242\. Design Neighbor Sum Service

Easy

You are given a `n x n` 2D array `grid` containing **distinct** elements in the range [0, n2 - 1].

Implement the `neighborSum` class:

*   `neighborSum(int [][]grid)` initializes the object.
*   `int adjacentSum(int value)` returns the **sum** of elements which are adjacent neighbors of `value`, that is either to the top, left, right, or bottom of `value` in `grid`.
*   `int diagonalSum(int value)` returns the **sum** of elements which are diagonal neighbors of `value`, that is either to the top-left, top-right, bottom-left, or bottom-right of `value` in `grid`.

![](https://assets.leetcode.com/uploads/2024/06/24/design.png)

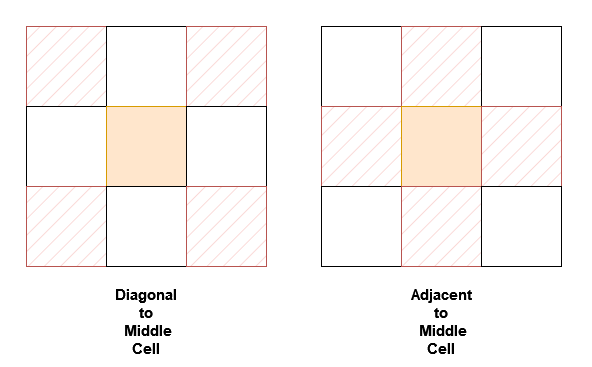
**Example 1:**

**Input:**

["neighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]

[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]

**Output:** [null, 6, 16, 16, 4]

**Explanation:**

**![](https://assets.leetcode.com/uploads/2024/06/24/designexample0.png)**

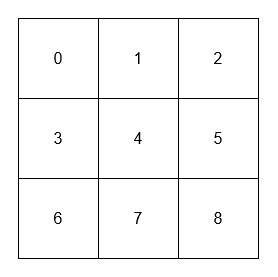*   The adjacent neighbors of 1 are 0, 2, and 4.
*   The adjacent neighbors of 4 are 1, 3, 5, and 7.
*   The diagonal neighbors of 4 are 0, 2, 6, and 8.
*   The diagonal neighbor of 8 is 4.

**Example 2:**

**Input:**

["neighborSum", "adjacentSum", "diagonalSum"]

[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]

**Output:** [null, 23, 45]

**Explanation:**

**![](https://assets.leetcode.com/uploads/2024/06/24/designexample2.png)**

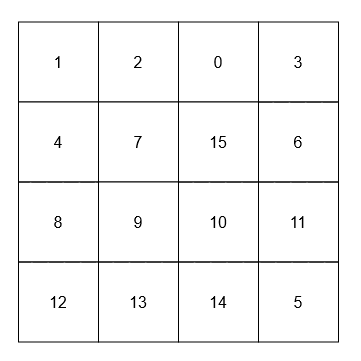*   The adjacent neighbors of 15 are 0, 10, 7, and 6.
*   The diagonal neighbors of 9 are 4, 12, 14, and 15.

**Constraints:**

*   `3 <= n == grid.length == grid[0].length <= 10`
*   0 <= grid[i][j] <= n2 - 1
*   All `grid[i][j]` are distinct.
*   `value` in `adjacentSum` and `diagonalSum` will be in the range [0, n2 - 1].
*   At most 2 * n2 calls will be made to `adjacentSum` and `diagonalSum`.