g1501_1600.s1572_matrix_diagonal_sum.Solution Maven / Gradle / Ivy

Go to download
package g1501_1600.s1572_matrix_diagonal_sum;

// #Easy #Array #Matrix #Programming_Skills_I_Day_7_Array #Udemy_2D_Arrays/Matrix
// #2022_04_11_Time_3_ms_(10.25%)_Space_48.3_MB_(26.47%)

import java.util.HashSet;
import java.util.Set;

/**
 * 1572 - Matrix Diagonal Sum\.
 *
 * Easy
 *
 * Given a square matrix `mat`, return the sum of the matrix diagonals.
 *
 * Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.
 *
 * **Example 1:**
 *
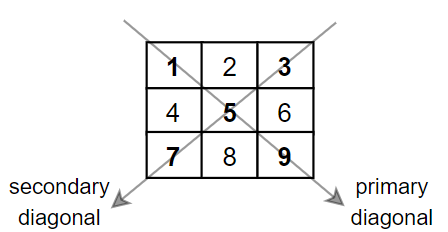
 * ![](https://assets.leetcode.com/uploads/2020/08/14/sample_1911.png)
 *
 * **Input:** mat = \[\[**1** ,2, **3** ], 
 *                   [4, **5** ,6], 
 *                   [**7** ,8, **9** ]]
 *
 * **Output:** 25
 *
 * **Explanation:** Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25 Notice that element mat[1][1] = 5 is counted only once.
 *
 * **Example 2:**
 *
 * **Input:** mat = \[\[**1** ,1,1, **1** ], 
 *                   [1, **1** , **1** ,1], 
 *                   [1, **1** , **1** ,1], 
 *                   [**1** ,1,1, **1** ]]
 *
 * **Output:** 8
 *
 * **Example 3:**
 *
 * **Input:** mat = \[\[**5** ]]
 *
 * **Output:** 5
 *
 * **Constraints:**
 *
 * *   `n == mat.length == mat[i].length`
 * *   `1 <= n <= 100`
 * *   `1 <= mat[i][j] <= 100`
**/
public class Solution {
    public int diagonalSum(int[][] mat) {
        int m = mat.length;
        Set added = new HashSet<>();
        int sum = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < m; j++) {
                if (i == j) {
                    added.add(i * m + j);
                    sum += mat[i][j];
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = m - 1; j >= 0; j--) {
                if (i + j == m - 1 && added.add(i * m + j)) {
                    sum += mat[i][j];
                }
            }
        }
        return sum;
    }
}