g1601_1700.s1631_path_with_minimum_effort.Solution Maven / Gradle / Ivy

Go to download
package g1601_1700.s1631_path_with_minimum_effort;

// #Medium #Array #Depth_First_Search #Breadth_First_Search #Binary_Search #Matrix
// #Heap_Priority_Queue #Union_Find #2022_04_19_Time_75_ms_(60.52%)_Space_42.8_MB_(86.40%)

import java.util.PriorityQueue;

/**
 * 1631 - Path With Minimum Effort\.
 *
 * Medium
 *
 * You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed** ). You can move **up** , **down** , **left** , or **right** , and you wish to find a route that requires the minimum **effort**.
 *
 * A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
 *
 * Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
 *
 * **Example 1:**
 *
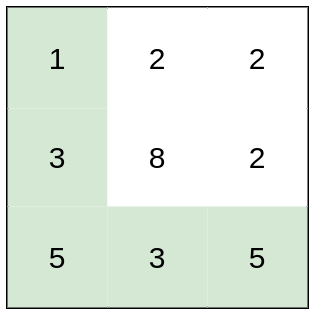
 * ![](https://assets.leetcode.com/uploads/2020/10/04/ex1.png)
 *
 * **Input:** heights = \[\[1,2,2],[3,8,2],[5,3,5]]
 *
 * **Output:** 2
 *
 * **Explanation:** The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells. This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
 *
 * **Example 2:**
 *
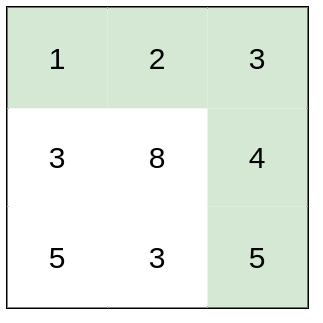
 * ![](https://assets.leetcode.com/uploads/2020/10/04/ex2.png)
 *
 * **Input:** heights = \[\[1,2,3],[3,8,4],[5,3,5]]
 *
 * **Output:** 1
 *
 * **Explanation:** The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
 *
 * **Example 3:**
 *
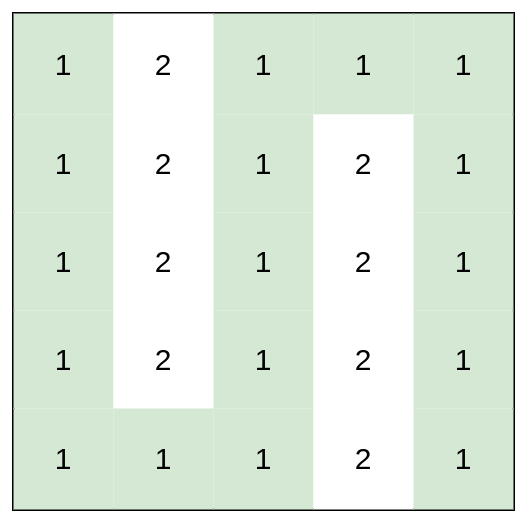
 * ![](https://assets.leetcode.com/uploads/2020/10/04/ex3.png)
 *
 * **Input:** heights = \[\[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
 *
 * **Output:** 0
 *
 * **Explanation:** This route does not require any effort.
 *
 * **Constraints:**
 *
 * *   `rows == heights.length`
 * *   `columns == heights[i].length`
 * *   `1 <= rows, columns <= 100`
 * *   1 <= heights[i][j] <= 10⁶
**/
@SuppressWarnings("java:S1210")
public class Solution {
    private static class Pair implements Comparable {
        int row;
        int col;
        int diff;

        Pair(int row, int col, int diff) {
            this.row = row;
            this.col = col;
            this.diff = diff;
        }

        public int compareTo(Pair o) {
            return this.diff - o.diff;
        }
    }

    public int minimumEffortPath(int[][] heights) {
        int n = heights.length;
        int m = heights[0].length;
        PriorityQueue pq = new PriorityQueue<>();
        pq.add(new Pair(0, 0, 0));
        boolean[][] vis = new boolean[n][m];
        int[] dx = {-1, 0, 1, 0};
        int[] dy = {0, 1, 0, -1};
        int min = Integer.MAX_VALUE;
        while (!pq.isEmpty()) {
            Pair p = pq.remove();
            int row = p.row;
            int col = p.col;
            int diff = p.diff;
            if (vis[row][col]) {
                continue;
            }
            vis[row][col] = true;
            if (row == n - 1 && col == m - 1) {
                min = Math.min(min, diff);
            }
            for (int i = 0; i < 4; i++) {
                int r = row + dx[i];
                int c = col + dy[i];
                if (r < 0 || c < 0 || r >= n || c >= m || vis[r][c]) {
                    continue;
                }
                pq.add(new Pair(r, c, Math.max(diff, Math.abs(heights[r][c] - heights[row][col]))));
            }
        }
        return min;
    }
}