g2301_2400.s2360_longest_cycle_in_a_graph.Solution Maven / Gradle / Ivy

Go to download
package g2301_2400.s2360_longest_cycle_in_a_graph;

// #Hard #Depth_First_Search #Graph #Topological_Sort
// #2022_08_14_Time_37_ms_(90.19%)_Space_102.8_MB_(72.92%)

/**
 * 2360 - Longest Cycle in a Graph\.
 *
 * Hard
 *
 * You are given a **directed** graph of `n` nodes numbered from `0` to `n - 1`, where each node has **at most one** outgoing edge.
 *
 * The graph is represented with a given **0-indexed** array `edges` of size `n`, indicating that there is a directed edge from node `i` to node `edges[i]`. If there is no outgoing edge from node `i`, then `edges[i] == -1`.
 *
 * Return _the length of the **longest** cycle in the graph_. If no cycle exists, return `-1`.
 *
 * A cycle is a path that starts and ends at the **same** node.
 *
 * **Example 1:**
 *
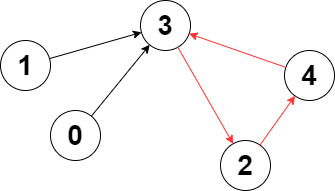
 * ![](https://assets.leetcode.com/uploads/2022/06/08/graph4drawio-5.png)
 *
 * **Input:** edges = [3,3,4,2,3]
 *
 * **Output:** 3
 *
 * **Explanation:** The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
 *
 * The length of this cycle is 3, so 3 is returned. 
 *
 * **Example 2:**
 *
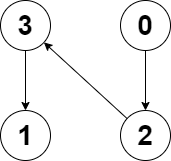
 * ![](https://assets.leetcode.com/uploads/2022/06/07/graph4drawio-1.png)
 *
 * **Input:** edges = [2,-1,3,1]
 *
 * **Output:** -1
 *
 * **Explanation:** There are no cycles in this graph. 
 *
 * **Constraints:**
 *
 * *   `n == edges.length`
 * *   2 <= n <= 10⁵
 * *   `-1 <= edges[i] < n`
 * *   `edges[i] != i`
**/
public class Solution {
    public int longestCycle(int[] edges) {
        int n = edges.length;
        boolean[] vis = new boolean[n];
        boolean[] dfsvis = new boolean[n];
        int[] path = new int[n];
        int maxLength = -1;
        for (int i = 0; i < n; i++) {
            if (!vis[i]) {
                path[i] = 1;
                maxLength = Math.max(maxLength, dfs(i, 1, path, vis, dfsvis, edges));
            }
        }
        return maxLength;
    }

    private int dfs(
            int node, int pathLength, int[] path, boolean[] vis, boolean[] dfsvis, int[] edges) {
        vis[node] = true;
        dfsvis[node] = true;
        int length = -1;
        if (edges[node] != -1 && !vis[edges[node]]) {
            path[edges[node]] = pathLength + 1;
            length = dfs(edges[node], pathLength + 1, path, vis, dfsvis, edges);
        } else if (edges[node] != -1 && dfsvis[edges[node]]) {
            length = pathLength - path[edges[node]] + 1;
        }
        dfsvis[node] = false;
        return length;
    }
}