g0301_0400.s0310_minimum_height_trees.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.41
package g0301_0400.s0310_minimum_height_trees;

// #Medium #Depth_First_Search #Breadth_First_Search #Graph #Topological_Sort
// #2022_07_07_Time_25_ms_(93.99%)_Space_72.4_MB_(71.31%)

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

/**
 * 310 - Minimum Height Trees\.
 *
 * Medium
 *
 * A tree is an undirected graph in which any two vertices are connected by _exactly_ one path. In other words, any connected graph without simple cycles is a tree.
 *
 * Given a tree of `n` nodes labelled from `0` to `n - 1`, and an array of `n - 1` `edges` where edges[i] = [a_i, b_i] indicates that there is an undirected edge between the two nodes a_i and b_i in the tree, you can choose any node of the tree as the root. When you select a node `x` as the root, the result tree has height `h`. Among all possible rooted trees, those with minimum height (i.e. `min(h)`) are called **minimum height trees** (MHTs).
 *
 * Return _a list of all **MHTs'** root labels_. You can return the answer in **any order**.
 *
 * The **height** of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
 *
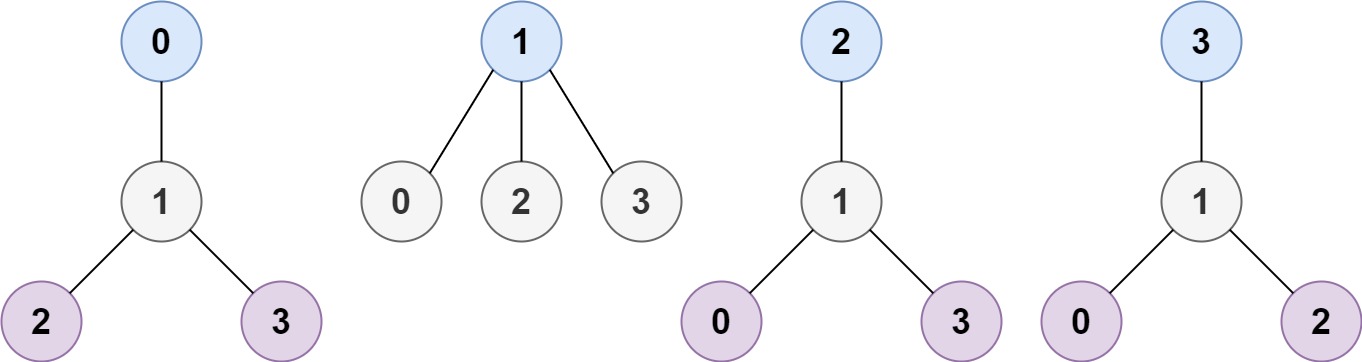
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/09/01/e1.jpg)
 *
 * **Input:** n = 4, edges = \[\[1,0],[1,2],[1,3]]
 *
 * **Output:** [1]
 *
 * **Explanation:** As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT. 
 *
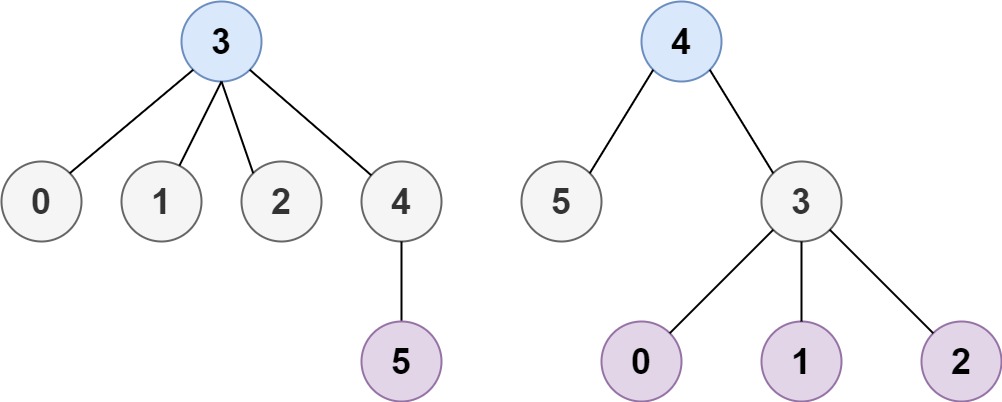
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/09/01/e2.jpg)
 *
 * **Input:** n = 6, edges = \[\[3,0],[3,1],[3,2],[3,4],[5,4]]
 *
 * **Output:** [3,4] 
 *
 * **Constraints:**
 *
 * *   1 <= n <= 2 * 10⁴
 * *   `edges.length == n - 1`
 * *   0 <= a_i, b_i < n
 * *   a_i != b_i
 * *   All the pairs (a_i, b_i) are distinct.
 * *   The given input is **guaranteed** to be a tree and there will be **no repeated** edges.
**/
@SuppressWarnings("unchecked")
public class Solution {
    public List findMinHeightTrees(int n, int[][] edges) {
        List answer = new ArrayList<>();
        if (n == 1) {
            answer.add(0);
            return answer;
        }
        List[] graph = new ArrayList[n];
        int[] degree = new int[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
            graph[edge[1]].add(edge[0]);
            degree[edge[0]]++;
            degree[edge[1]]++;
        }
        Queue leaf = new LinkedList<>();
        int remainingNodes = n;
        for (int i = 0; i < n; i++) {
            if (degree[i] == 1) {
                leaf.add(i);
            }
        }
        while (!leaf.isEmpty()) {
            // We found answer if queue left with <=2 elements
            if (remainingNodes <= 2) {
                break;
            }
            int size = leaf.size();
            while (--size >= 0) {
                int l = leaf.poll();
                remainingNodes--;
                for (int adj : graph[l]) {
                    // edge is removed so degree will decrease for both vertex
                    degree[adj]--;
                    if (degree[adj] == 1) {
                        leaf.add(adj);
                    }
                }
            }
        }
        answer.addAll(leaf);
        return answer;
    }
}