g0601_0700.s0684_redundant_connection.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.41

package g0601_0700.s0684_redundant_connection;

// #Medium #Depth_First_Search #Breadth_First_Search #Graph #Union_Find
// #2022_03_22_Time_0_ms_(100.00%)_Space_42.7_MB_(76.10%)

/**
 * 684 - Redundant Connection\.
 *
 * Medium
 *
 * In this problem, a tree is an **undirected graph** that is connected and has no cycles.
 *
 * You are given a graph that started as a tree with `n` nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array `edges` of length `n` where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the graph.
 *
 * Return _an edge that can be removed so that the resulting graph is a tree of_ `n` _nodes_. If there are multiple answers, return the answer that occurs last in the input.
 *
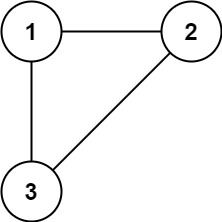
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/05/02/reduntant1-1-graph.jpg)
 *
 * **Input:** edges = \[\[1,2],[1,3],[2,3]]
 *
 * **Output:** [2,3]
 *
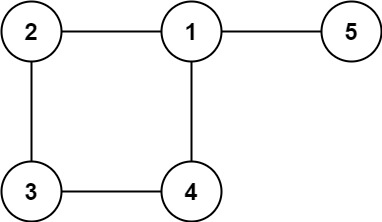
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/05/02/reduntant1-2-graph.jpg)
 *
 * **Input:** edges = \[\[1,2],[2,3],[3,4],[1,4],[1,5]]
 *
 * **Output:** [1,4]
 *
 * **Constraints:**
 *
 * *   `n == edges.length`
 * *   `3 <= n <= 1000`
 * *   `edges[i].length == 2`
 * *   1 <= a_i < b_i <= edges.length
 * *   a_i != b_i
 * *   There are no repeated edges.
 * *   The given graph is connected.
**/
public class Solution {
    private int[] par;

    public int[] findRedundantConnection(int[][] edges) {
        int[] ans = new int[2];
        int n = edges.length;
        par = new int[n + 1];
        for (int i = 0; i < n; i++) {
            par[i] = i;
        }
        for (int[] edge : edges) {
            int lx = find(edge[0]);
            int ly = find(edge[1]);
            if (lx != ly) {
                par[lx] = ly;
            } else {
                ans[0] = edge[0];
                ans[1] = edge[1];
            }
        }
        return ans;
    }

    private int find(int x) {
        if (par[x] == x) {
            return x;
        }
        return find(par[x]);
    }
}