g0601_0700.s0699_falling_squares.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g0601_0700.s0699_falling_squares;

// #Hard #Array #Ordered_Set #Segment_Tree #2022_03_22_Time_8_ms_(91.03%)_Space_42.8_MB_(90.38%)

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Set;
import java.util.TreeSet;

/**
 * 699 - Falling Squares\.
 *
 * Hard
 *
 * There are several squares being dropped onto the X-axis of a 2D plane.
 *
 * You are given a 2D integer array `positions` where positions[i] = [left_i, sideLength_i] represents the i^th square with a side length of sideLength_i that is dropped with its left edge aligned with X-coordinate left_i.
 *
 * Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
 *
 * After each square is dropped, you must record the **height of the current tallest stack of squares**.
 *
 * Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ i^th _square_.
 *
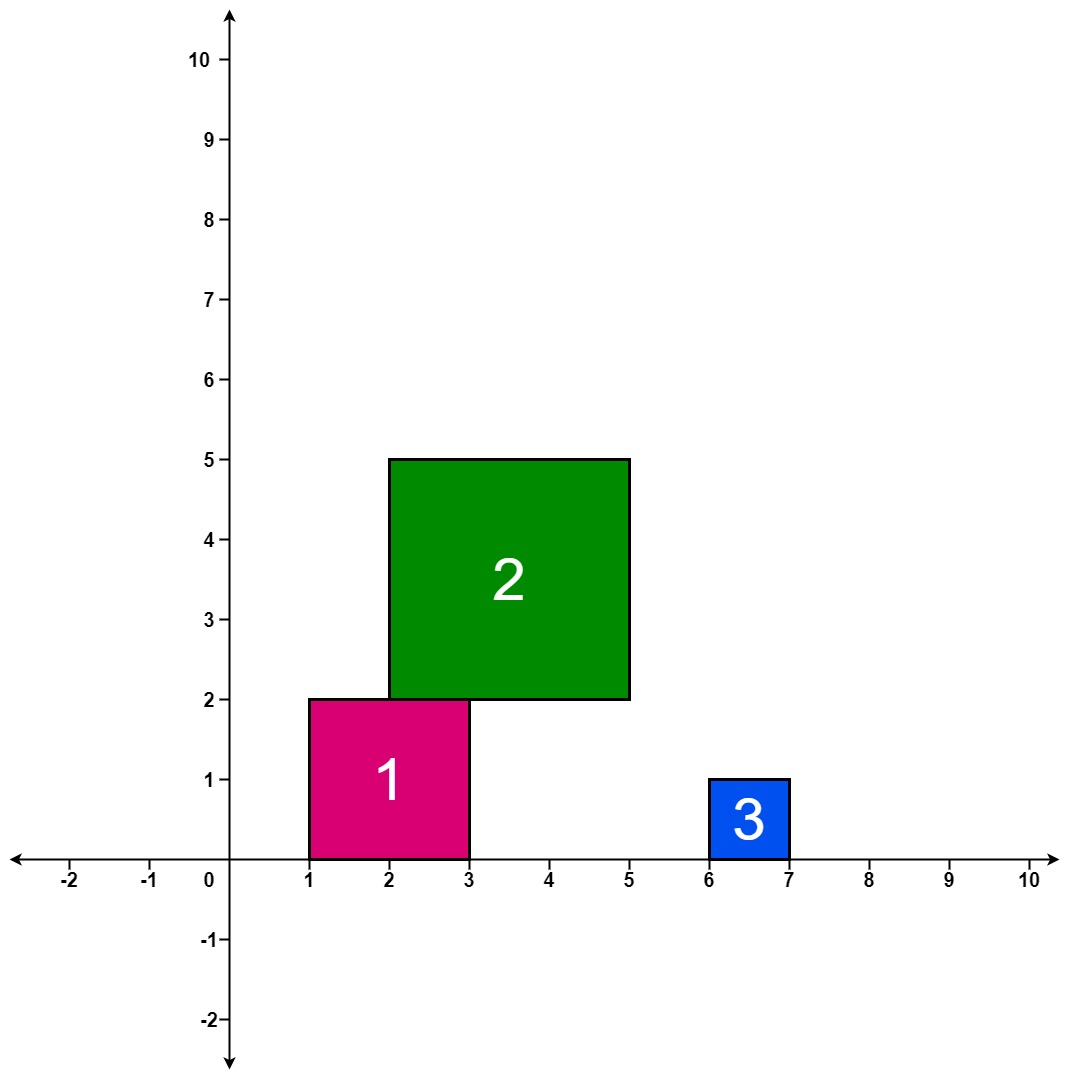
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/04/28/fallingsq1-plane.jpg)
 *
 * **Input:** positions = \[\[1,2],[2,3],[6,1]]
 *
 * **Output:** [2,5,5]
 *
 * **Explanation:**
 *
 * After the first drop, the tallest stack is square 1 with a height of 2.
 *
 * After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
 *
 * After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
 *
 * Thus, we return an answer of [2, 5, 5]. 
 *
 * **Example 2:**
 *
 * **Input:** positions = \[\[100,100],[200,100]]
 *
 * **Output:** [100,100]
 *
 * **Explanation:**
 *
 * After the first drop, the tallest stack is square 1 with a height of 100.
 *
 * After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
 *
 * Thus, we return an answer of [100, 100].
 *
 * Note that square 2 only brushes the right side of square 1, which does not count as landing on it. 
 *
 * **Constraints:**
 *
 * *   `1 <= positions.length <= 1000`
 * *   1 <= left_i <= 10⁸
 * *   1 <= sideLength_i <= 10⁶
**/
public class Solution {
    public List fallingSquares(int[][] positions) {
        // Coordinate compression using TreeSet
        Set unique = new TreeSet<>();
        for (int[] square : positions) {
            unique.add(square[0]);
            unique.add(square[0] + square[1] - 1);
        }
        // converted the TreeSet to a List
        List sorted = new ArrayList<>(unique);
        // Storing the max heights for compressed coordinates
        int[] heights = new int[sorted.size()];
        // Our answer list
        List list = new ArrayList<>(positions.length);
        // Global Max
        int max = 0;
        for (int[] square : positions) {
            // coordinate compression lookup
            int x1 = Collections.binarySearch(sorted, square[0]);
            int x2 = Collections.binarySearch(sorted, square[0] + square[1] - 1);
            // get the current max for the interval between x1 and x2
            int current = 0;
            for (int i = x1; i <= x2; i++) {
                current = Math.max(current, heights[i]);
            }
            // add the new square on the top
            current += square[1];
            // update the interval with the new value
            for (int i = x1; i <= x2; i++) {
                heights[i] = current;
            }
            // recalculate the global max
            max = Math.max(max, current);
            list.add(max);
        }
        return list;
    }
}