g0701_0800.s0764_largest_plus_sign.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g0701_0800.s0764_largest_plus_sign;

// #Medium #Array #Dynamic_Programming #2022_03_26_Time_39_ms_(87.23%)_Space_53.3_MB_(82.98%)

/**
 * 764 - Largest Plus Sign\.
 *
 * Medium
 *
 * You are given an integer `n`. You have an `n x n` binary grid `grid` with all values initially `1`'s except for some indices given in the array `mines`. The i^th element of the array `mines` is defined as mines[i] = [x_i, y_i] where grid[x_i][y_i] == 0.
 *
 * Return _the order of the largest **axis-aligned** plus sign of_ 1_'s contained in_ `grid`. If there is none, return `0`.
 *
 * An **axis-aligned plus sign** of `1`'s of order `k` has some center `grid[r][c] == 1` along with four arms of length `k - 1` going up, down, left, and right, and made of `1`'s. Note that there could be `0`'s or `1`'s beyond the arms of the plus sign, only the relevant area of the plus sign is checked for `1`'s.
 *
 * **Example 1:**
 *
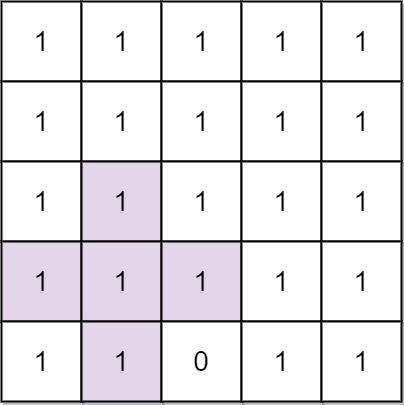
 * ![](https://assets.leetcode.com/uploads/2021/06/13/plus1-grid.jpg)
 *
 * **Input:** n = 5, mines = \[\[4,2]]
 *
 * **Output:** 2
 *
 * **Explanation:** In the above grid, the largest plus sign can only be of order 2. One of them is shown.
 *
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/06/13/plus2-grid.jpg)
 *
 * **Input:** n = 1, mines = \[\[0,0]]
 *
 * **Output:** 0
 *
 * **Explanation:** There is no plus sign, so return 0.
 *
 * **Constraints:**
 *
 * *   `1 <= n <= 500`
 * *   `1 <= mines.length <= 5000`
 * *   0 <= x_i, y_i < n
 * *   All the pairs (x_i, y_i) are **unique**.
**/
public class Solution {
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        boolean[][] mat = new boolean[n][n];
        for (int[] pos : mines) {
            mat[pos[0]][pos[1]] = true;
        }
        int[][] left = new int[n][n];
        int[][] right = new int[n][n];
        int[][] up = new int[n][n];
        int[][] down = new int[n][n];
        int ans = 0;
        // For Left and Up only
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                int i1 = j == 0 ? 0 : left[i][j - 1];
                left[i][j] = mat[i][j] ? 0 : 1 + i1;
                int i2 = i == 0 ? 0 : up[i - 1][j];
                up[i][j] = mat[i][j] ? 0 : 1 + i2;
            }
        }
        // For Right and Down and simoultaneously get answer
        for (int i = n - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                int i1 = j == n - 1 ? 0 : right[i][j + 1];
                right[i][j] = mat[i][j] ? 0 : 1 + i1;
                int i2 = i == n - 1 ? 0 : down[i + 1][j];
                down[i][j] = mat[i][j] ? 0 : 1 + i2;
                int x = Math.min(Math.min(left[i][j], up[i][j]), Math.min(right[i][j], down[i][j]));
                ans = Math.max(ans, x);
            }
        }
        return ans;
    }
}