g0701_0800.s0778_swim_in_rising_water.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g0701_0800.s0778_swim_in_rising_water;

// #Hard #Array #Depth_First_Search #Breadth_First_Search #Binary_Search #Matrix
// #Heap_Priority_Queue #Union_Find #2022_03_26_Time_13_ms_(69.75%)_Space_51.8_MB_(12.57%)

import java.util.LinkedList;
import java.util.Queue;

/**
 * 778 - Swim in Rising Water\.
 *
 * Hard
 *
 * You are given an `n x n` integer matrix `grid` where each value `grid[i][j]` represents the elevation at that point `(i, j)`.
 *
 * The rain starts to fall. At time `t`, the depth of the water everywhere is `t`. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most `t`. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
 *
 * Return _the least time until you can reach the bottom right square_ `(n - 1, n - 1)` _if you start at the top left square_ `(0, 0)`.
 *
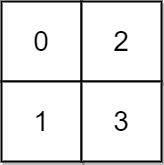
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/06/29/swim1-grid.jpg)
 *
 * **Input:** grid = \[\[0,2],[1,3]]
 *
 * **Output:** 3
 *
 * **Explanation:**
 *
 *     At time 0, you are in grid location (0, 0).
 *     You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
 *     You cannot reach point (1, 1) until time 3.
 *     When the depth of water is 3, we can swim anywhere inside the grid. 
 *
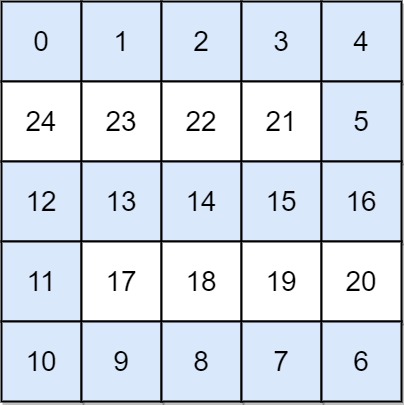
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/06/29/swim2-grid-1.jpg)
 *
 * **Input:** grid = \[\[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
 *
 * **Output:** 16
 *
 * **Explanation:**
 *
 *     The final route is shown.
 *     We need to wait until time 16 so that (0, 0) and (4, 4) are connected. 
 *
 * **Constraints:**
 *
 * *   `n == grid.length`
 * *   `n == grid[i].length`
 * *   `1 <= n <= 50`
 * *   0 <= grid[i][j] < n²
 * *   Each value `grid[i][j]` is **unique**.
**/
public class Solution {
    private int[] dir = new int[] {-1, 0, 1, 0, -1};

    public int swimInWater(int[][] grid) {
        int max = 0;
        // find the maximum value in the matrix
        for (int[] ints : grid) {
            for (int j = 0; j < grid[0].length; j++) {
                max = Math.max(max, ints[j]);
            }
        }
        int l = 0;
        int r = max;
        int res = 0;
        // perform binary search
        while (l <= r) {
            // find test water level
            int mid = (l + r) / 2;
            // if you can reach destination with current water level, store it as an answer and try
            // lowering water level
            if (bfs(grid, mid)) {
                res = mid;
                r = mid - 1;
            } else {
                // otherwise increase water level and try again
                l = mid + 1;
            }
        }
        return res;
    }

    public boolean bfs(int[][] grid, int limit) {
        // use queue to process cells starting from top left corner
        Queue que = new LinkedList<>();
        // boolean array to keep track of visited cells
        boolean[][] visited = new boolean[grid.length][grid[0].length];
        // we start from top left corner
        que.add(new int[] {0, 0});
        visited[0][0] = true;
        while (!que.isEmpty()) {
            // get current cell
            int[] cur = que.poll();
            int x = cur[0];
            int y = cur[1];
            // if value of current cell is greater than limit return false
            if (grid[x][y] > limit) {
                return false;
            }
            // if we reached the destination return true
            if (x == grid.length - 1 && y == grid[0].length - 1) {
                return true;
            }
            // check cells in all 4 directions
            for (int i = 0; i < dir.length - 1; i++) {
                int dx = x + dir[i];
                int dy = y + dir[i + 1];
                // if neighboring cell is in bounds, and hasn't been visited yet,
                // and its value is less than current water level, add it to visited array and to
                // the queue
                if (dx >= 0
                        && dy >= 0
                        && dx < grid.length
                        && dy < grid[0].length
                        && !visited[dx][dy]
                        && grid[dx][dy] <= limit) {
                    visited[dx][dy] = true;
                    que.add(new int[] {dx, dy});
                }
            }
        }
        return false;
    }
}