g0701_0800.s0785_is_graph_bipartite.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g0701_0800.s0785_is_graph_bipartite;

// #Medium #Depth_First_Search #Breadth_First_Search #Graph #Union_Find
// #Graph_Theory_I_Day_14_Graph_Theory #2022_03_26_Time_0_ms_(100.00%)_Space_54.3_MB_(18.06%)

/**
 * 785 - Is Graph Bipartite?\.
 *
 * Medium
 *
 * There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
 *
 * *   There are no self-edges (`graph[u]` does not contain `u`).
 * *   There are no parallel edges (`graph[u]` does not contain duplicate values).
 * *   If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
 * *   The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
 *
 * A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
 *
 * Return `true` _if and only if it is **bipartite**_.
 *
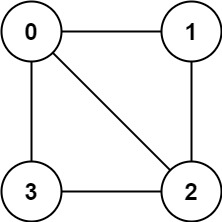
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/10/21/bi2.jpg)
 *
 * **Input:** graph = \[\[1,2,3],[0,2],[0,1,3],[0,2]]
 *
 * **Output:** false
 *
 * **Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
 *
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/10/21/bi1.jpg)
 *
 * **Input:** graph = \[\[1,3],[0,2],[1,3],[0,2]]
 *
 * **Output:** true
 *
 * **Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
 *
 * **Constraints:**
 *
 * *   `graph.length == n`
 * *   `1 <= n <= 100`
 * *   `0 <= graph[u].length < n`
 * *   `0 <= graph[u][i] <= n - 1`
 * *   `graph[u]` does not contain `u`.
 * *   All the values of `graph[u]` are **unique**.
 * *   If `graph[u]` contains `v`, then `graph[v]` contains `u`.
**/
public class Solution {
    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        int[] color = new int[n];
        for (int i = 0; i < n; i++) {
            if (color[i] == 0 && !helper(graph, i, -1, color)) {
                return false;
            }
        }
        return true;
    }

    private boolean helper(int[][] graph, int curr, int c, int[] color) {
        if (color[curr] == c) {
            return true;
        }
        color[curr] = c;
        for (int x : graph[curr]) {
            if (color[x] == c || !helper(graph, x, c * -1, color)) {
                return false;
            }
        }
        return true;
    }
}