g0701_0800.s0787_cheapest_flights_within_k_stops.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g0701_0800.s0787_cheapest_flights_within_k_stops;

// #Medium #Dynamic_Programming #Depth_First_Search #Breadth_First_Search #Heap_Priority_Queue
// #Graph #Shortest_Path #2022_03_26_Time_9_ms_(53.93%)_Space_46.9_MB_(59.68%)

import java.util.Arrays;

/**
 * 787 - Cheapest Flights Within K Stops\.
 *
 * Medium
 *
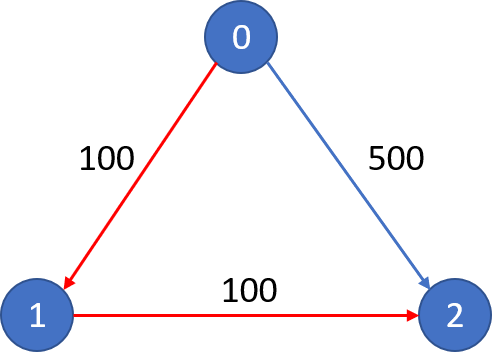
 * There are `n` cities connected by some number of flights. You are given an array `flights` where flights[i] = [from_i, to_i, price_i] indicates that there is a flight from city from_i to city to_i with cost price_i.
 *
 * You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
 *
 * **Example 1:**
 *
 * ![](https://s3-lc-upload.s3.amazonaws.com/uploads/2018/02/16/995.png)
 *
 * **Input:** n = 3, flights = \[\[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
 *
 * **Output:** 200
 *
 * **Explanation:**
 *
 * The graph is shown.
 *
 * The cheapest price from city `0` to city `2` with at most 1 stop costs 200, as marked red in the picture. 
 *
 * **Example 2:**
 *
 * ![](https://s3-lc-upload.s3.amazonaws.com/uploads/2018/02/16/995.png)
 *
 * **Input:** n = 3, flights = \[\[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
 *
 * **Output:** 500
 *
 * **Explanation:**
 *
 * The graph is shown.
 *
 * The cheapest price from city `0` to city `2` with at most 0 stop costs 500, as marked blue in the picture. 
 *
 * **Constraints:**
 *
 * *   `1 <= n <= 100`
 * *   `0 <= flights.length <= (n * (n - 1) / 2)`
 * *   `flights[i].length == 3`
 * *   0 <= from_i, to_i < n
 * *   from_i != to_i
 * *   1 <= price_i <= 10⁴
 * *   There will not be any multiple flights between two cities.
 * *   `0 <= src, dst, k < n`
 * *   `src != dst`
**/
public class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        // k + 2 becase there are total of k(intermediate stops) + 1(src) + 1(dst)
        // dp[i][j] = cost to reach j using atmost i edges from src
        int[][] dp = new int[k + 2][n];
        for (int[] row : dp) {
            Arrays.fill(row, Integer.MAX_VALUE);
        }
        // cost to reach src is always 0
        for (int i = 0; i <= k + 1; i++) {
            dp[i][src] = 0;
        }
        // k+1 because k stops + dst
        for (int i = 1; i <= k + 1; i++) {
            for (int[] flight : flights) {
                int srcAirport = flight[0];
                int destAirport = flight[1];
                int cost = flight[2];
                // if cost to reach srcAirport in i - 1 steps is already found out then
                // the cost to reach destAirport will be min(cost to reach destAirport computed
                // already from some other srcAirport OR cost to reach srcAirport in i - 1 steps +
                // the cost to reach destAirport from srcAirport)
                if (dp[i - 1][srcAirport] != Integer.MAX_VALUE) {
                    dp[i][destAirport] = Math.min(dp[i][destAirport], dp[i - 1][srcAirport] + cost);
                }
            }
        }
        // checking for dp[k + 1][dst] because there are 'k + 2' airports in a path and distance
        // covered between 'k + 2' airports is 'k + 1'
        return dp[k + 1][dst] == Integer.MAX_VALUE ? -1 : dp[k + 1][dst];
    }
}