g0801_0900.s0834_sum_of_distances_in_tree.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g0801_0900.s0834_sum_of_distances_in_tree;

// #Hard #Dynamic_Programming #Depth_First_Search #Tree #Graph
// #2022_03_24_Time_52_ms_(91.09%)_Space_96.7_MB_(75.86%)

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 834 - Sum of Distances in Tree\.
 *
 * Hard
 *
 * There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
 *
 * You are given the integer `n` and the array `edges` where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.
 *
 * Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the i^th node in the tree and all other nodes.
 *
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/07/23/lc-sumdist1.jpg)
 *
 * **Input:** n = 6, edges = \[\[0,1],[0,2],[2,3],[2,4],[2,5]]
 *
 * **Output:** [8,12,6,10,10,10]
 *
 * **Explanation:** The tree is shown above. 
 *
 * We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) equals 1 + 1 + 2 + 2 + 2 = 8. 
 *
 * Hence, answer[0] = 8, and so on.
 *
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/07/23/lc-sumdist2.jpg)
 *
 * **Input:** n = 1, edges = []
 *
 * **Output:** [0]
 *
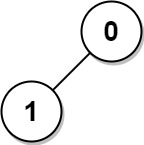
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/07/23/lc-sumdist3.jpg)
 *
 * **Input:** n = 2, edges = \[\[1,0]]
 *
 * **Output:** [1,1]
 *
 * **Constraints:**
 *
 * *   1 <= n <= 3 * 10⁴
 * *   `edges.length == n - 1`
 * *   `edges[i].length == 2`
 * *   0 <= a_i, b_i < n
 * *   a_i != b_i
 * *   The given input represents a valid tree.
**/
@SuppressWarnings("unchecked")
public class Solution {
    private int n;
    private int[] count;
    private int[] answer;
    private List[] graph;

    private void postorder(int node, int parent) {
        for (int child : graph[node]) {
            if (child != parent) {
                postorder(child, node);
                count[node] += count[child];
                answer[node] += answer[child] + count[child];
            }
        }
    }

    private void preorder(int node, int parent) {

        for (int child : graph[node]) {
            if (child != parent) {
                answer[child] = answer[node] - count[child] + n - count[child];
                preorder(child, node);
            }
        }
    }

    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        this.n = n;
        count = new int[n];
        answer = new int[n];
        graph = new List[n];
        Arrays.fill(count, 1);
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
            graph[edge[1]].add(edge[0]);
        }
        postorder(0, -1);
        preorder(0, -1);
        return answer;
    }
}