
g0801_0900.s0883_projection_area_of_3d_shapes.Solution Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
package g0801_0900.s0883_projection_area_of_3d_shapes;
// #Easy #Array #Math #Matrix #Geometry #2022_03_28_Time_1_ms_(100.00%)_Space_44.8_MB_(37.40%)
/**
* 883 - Projection Area of 3D Shapes\.
*
* Easy
*
* You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
*
* Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
*
* We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
*
* A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow" when looking at the cubes from the top, the front, and the side.
*
* Return _the total area of all three projections_.
*
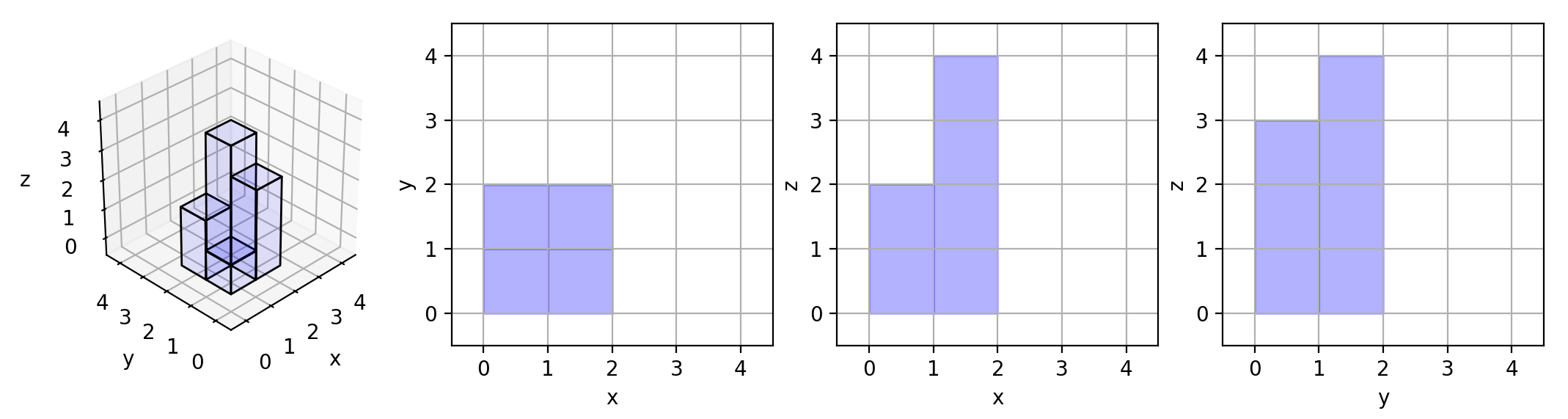
* **Example 1:**
*
* 
*
* **Input:** grid = \[\[1,2],[3,4]]
*
* **Output:** 17
*
* **Explanation:** Here are the three projections ("shadows") of the shape made with each axis-aligned plane.
*
* **Example 2:**
*
* **Input:** grid = \[\[2]]
*
* **Output:** 5
*
* **Example 3:**
*
* **Input:** grid = \[\[1,0],[0,2]]
*
* **Output:** 8
*
* **Constraints:**
*
* * `n == grid.length == grid[i].length`
* * `1 <= n <= 50`
* * `0 <= grid[i][j] <= 50`
**/
public class Solution {
public int projectionArea(int[][] grid) {
int n = grid.length;
int m = grid[0].length;
int sum = n * m;
int count = 0;
for (int[] ints : grid) {
int max = Integer.MIN_VALUE;
for (int j = 0; j < m; j++) {
if (ints[j] == 0) {
count++;
}
if (max < ints[j]) {
max = ints[j];
}
}
sum += max;
}
for (int i = 0; i < n; i++) {
int max = Integer.MIN_VALUE;
for (int j = 0; j < m; j++) {
if (max < grid[j][i]) {
max = grid[j][i];
}
}
sum += max;
}
return sum - count;
}
}
© 2015 - 2025 Weber Informatics LLC | Privacy Policy