g0901_1000.s0913_cat_and_mouse.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g0901_1000.s0913_cat_and_mouse;

// #Hard #Dynamic_Programming #Math #Graph #Memoization #Topological_Sort #Game_Theory
// #2022_03_29_Time_16_ms_(97.20%)_Space_47_MB_(78.40%)

import java.util.LinkedList;
import java.util.Queue;

/**
 * 913 - Cat and Mouse\.
 *
 * Hard
 *
 * A game on an **undirected** graph is played by two players, Mouse and Cat, who alternate turns.
 *
 * The graph is given as follows: `graph[a]` is a list of all nodes `b` such that `ab` is an edge of the graph.
 *
 * The mouse starts at node `1` and goes first, the cat starts at node `2` and goes second, and there is a hole at node `0`.
 *
 * During each player's turn, they **must** travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it **must** travel to any node in `graph[1]`.
 *
 * Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)
 *
 * Then, the game can end in three ways:
 *
 * *   If ever the Cat occupies the same node as the Mouse, the Cat wins.
 * *   If ever the Mouse reaches the Hole, the Mouse wins.
 * *   If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw.
 *
 * Given a `graph`, and assuming both players play optimally, return
 *
 * *   `1` if the mouse wins the game,
 * *   `2` if the cat wins the game, or
 * *   `0` if the game is a draw.
 *
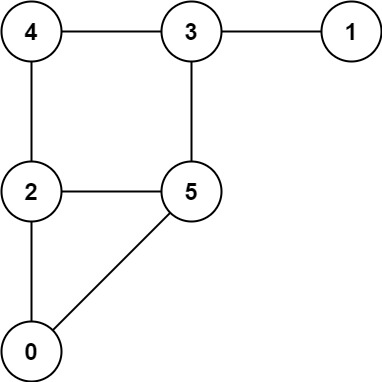
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/11/17/cat1.jpg)
 *
 * **Input:** graph = \[\[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
 *
 * **Output:** 0
 *
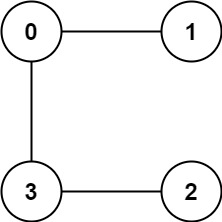
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/11/17/cat2.jpg)
 *
 * **Input:** graph = \[\[1,3],[0],[3],[0,2]]
 *
 * **Output:** 1
 *
 * **Constraints:**
 *
 * *   `3 <= graph.length <= 50`
 * *   `1 <= graph[i].length < graph.length`
 * *   `0 <= graph[i][j] < graph.length`
 * *   `graph[i][j] != i`
 * *   `graph[i]` is unique.
 * *   The mouse and the cat can always move.
**/
public class Solution {
    private static final int DRAW = 0;
    private static final int MOUSE_WIN = 1;
    private static final int CAT_WIN = 2;
    private static final int MOUSE = 0;
    private static final int CAT = 1;

    public int catMouseGame(int[][] graph) {
        int n = graph.length;
        int[][][] states = new int[n][n][2];
        int[][][] degree = new int[n][n][2];
        for (int m = 0; m < n; ++m) {
            for (int c = 0; c < n; ++c) {
                degree[m][c][MOUSE] = graph[m].length;
                degree[m][c][CAT] = graph[c].length;
                for (int node : graph[c]) {
                    if (node == 0) {
                        --degree[m][c][CAT];
                        break;
                    }
                }
            }
        }
        Queue q = new LinkedList<>();
        for (int i = 1; i < n; ++i) {
            states[0][i][MOUSE] = MOUSE_WIN;
            states[0][i][CAT] = MOUSE_WIN;
            states[i][i][MOUSE] = CAT_WIN;
            states[i][i][CAT] = CAT_WIN;
            q.offer(new int[] {0, i, MOUSE, MOUSE_WIN});
            q.offer(new int[] {i, i, MOUSE, CAT_WIN});
            q.offer(new int[] {0, i, CAT, MOUSE_WIN});
            q.offer(new int[] {i, i, CAT, CAT_WIN});
        }
        while (!q.isEmpty()) {
            int[] state = q.poll();
            int mouse = state[0];
            int cat = state[1];
            int turn = state[2];
            int result = state[3];
            if (mouse == 1 && cat == 2 && turn == MOUSE) {
                return result;
            }
            int prevTurn = 1 - turn;
            for (int prev : graph[prevTurn == MOUSE ? mouse : cat]) {
                int prevMouse = prevTurn == MOUSE ? prev : mouse;
                int prevCat = prevTurn == CAT ? prev : cat;
                if (prevCat != 0
                        && states[prevMouse][prevCat][prevTurn] == DRAW
                        && (prevTurn == MOUSE && result == MOUSE_WIN
                                || prevTurn == CAT && result == CAT_WIN
                                || --degree[prevMouse][prevCat][prevTurn] == 0)) {
                    states[prevMouse][prevCat][prevTurn] = result;
                    q.offer(new int[] {prevMouse, prevCat, prevTurn, result});
                }
            }
        }
        return DRAW;
    }
}