g0901_1000.s0935_knight_dialer.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.41
package g0901_1000.s0935_knight_dialer;

// #Medium #Dynamic_Programming #2022_03_30_Time_4_ms_(99.08%)_Space_42.2_MB_(81.87%)

import java.util.ArrayList;
import java.util.List;

/**
 * 935 - Knight Dialer\.
 *
 * Medium
 *
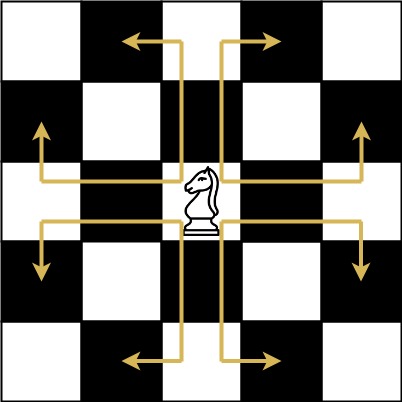
 * The chess knight has a **unique movement** , it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L** ). The possible movements of chess knight are shown in this diagaram:
 *
 * A chess knight can move as indicated in the chess diagram below:
 *
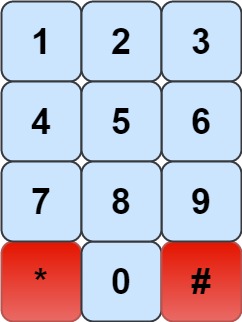
 * ![](https://assets.leetcode.com/uploads/2020/08/18/chess.jpg)
 *
 * We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
 *
 * ![](https://assets.leetcode.com/uploads/2020/08/18/phone.jpg)
 *
 * Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
 *
 * You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
 *
 * As the answer may be very large, **return the answer modulo** 10⁹ + 7.
 *
 * **Example 1:**
 *
 * **Input:** n = 1
 *
 * **Output:** 10
 *
 * **Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
 *
 * **Example 2:**
 *
 * **Input:** n = 2
 *
 * **Output:** 20
 *
 * **Explanation:** All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
 *
 * **Example 3:**
 *
 * **Input:** n = 3131
 *
 * **Output:** 136006598
 *
 * **Explanation:** Please take care of the mod.
 *
 * **Constraints:**
 *
 * *   `1 <= n <= 5000`
**/
public class Solution {
    private static final int[][] MAP = new int[10][];
    private static final List MEMO = new ArrayList<>();

    static {
        MAP[0] = new int[] {4, 6};
        MAP[1] = new int[] {6, 8};
        MAP[2] = new int[] {7, 9};
        MAP[3] = new int[] {4, 8};
        MAP[4] = new int[] {3, 9, 0};
        MAP[5] = new int[0];
        MAP[6] = new int[] {1, 7, 0};
        MAP[7] = new int[] {2, 6};
        MAP[8] = new int[] {1, 3};
        MAP[9] = new int[] {2, 4};
        MEMO.add(new int[] {1, 1, 1, 1, 1, 0, 1, 1, 1, 1});
    }

    public int knightDialer(int n) {
        if (n == 1) {
            return 10;
        }
        int mod = 1000_000_007;
        while (MEMO.size() < n) {
            int[] cur = MEMO.get(MEMO.size() - 1);
            int[] next = new int[10];
            for (int i = 0; i < 10; i++) {
                for (int d : MAP[i]) {
                    next[d] = (next[d] + cur[i]) % mod;
                }
            }
            MEMO.add(next);
        }
        int sum = 0;
        for (int x : MEMO.get(n - 1)) {
            sum = (sum + x) % mod;
        }
        return sum;
    }
}