g1001_1100.s1035_uncrossed_lines.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g1001_1100.s1035_uncrossed_lines;

// #Medium #Array #Dynamic_Programming #2022_02_27_Time_5_ms_(85.32%)_Space_45.3_MB_(5.21%)

/**
 * 1035 - Uncrossed Lines\.
 *
 * Medium
 *
 * You are given two integer arrays `nums1` and `nums2`. We write the integers of `nums1` and `nums2` (in the order they are given) on two separate horizontal lines.
 *
 * We may draw connecting lines: a straight line connecting two numbers `nums1[i]` and `nums2[j]` such that:
 *
 * *   `nums1[i] == nums2[j]`, and
 * *   the line we draw does not intersect any other connecting (non-horizontal) line.
 *
 * Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
 *
 * Return _the maximum number of connecting lines we can draw in this way_.
 *
 * **Example 1:**
 *
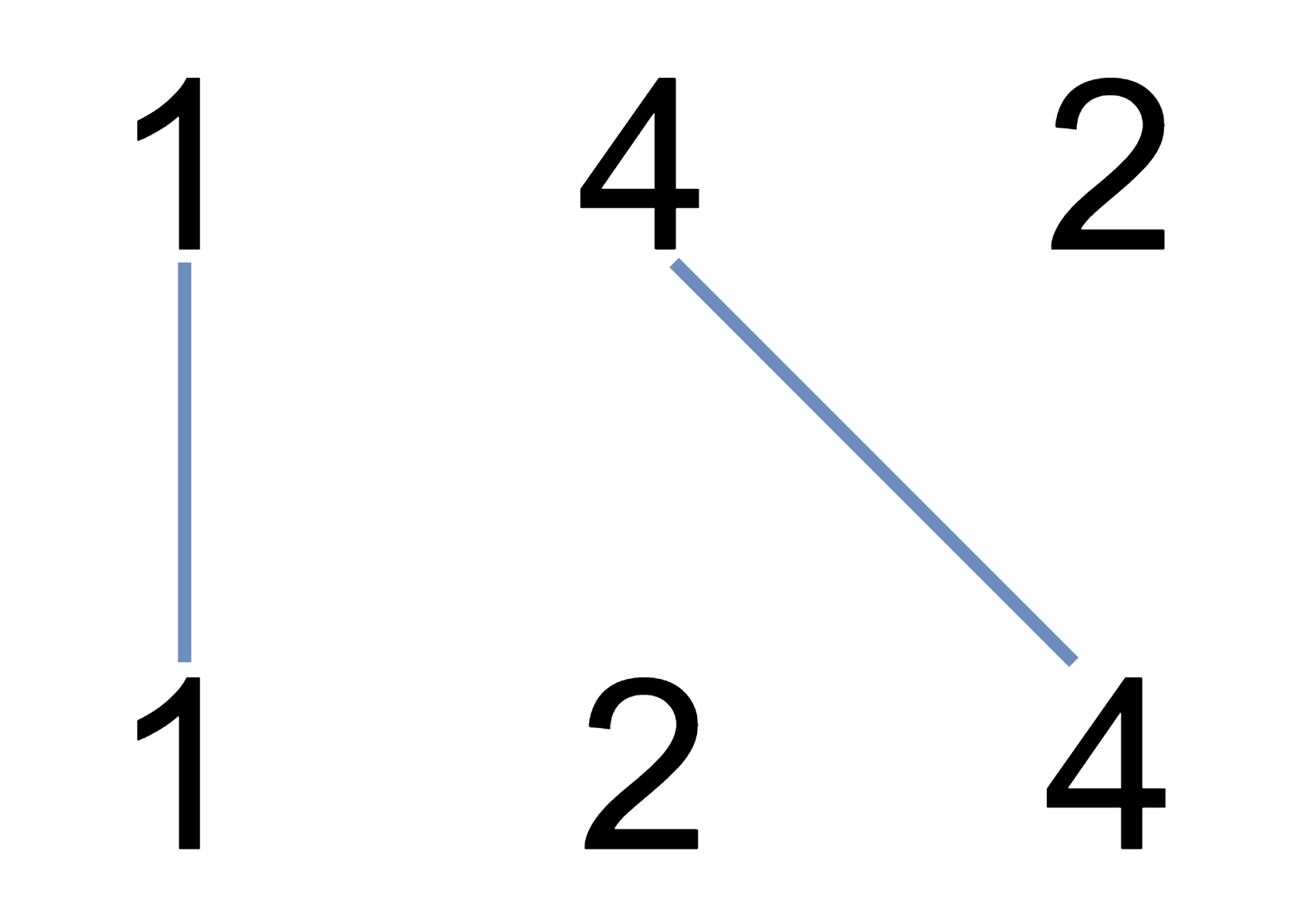
 * ![](https://assets.leetcode.com/uploads/2019/04/26/142.png)
 *
 * **Input:** nums1 = [1,4,2], nums2 = [1,2,4]
 *
 * **Output:** 2
 *
 * **Explanation:** We can draw 2 uncrossed lines as in the diagram. We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.
 *
 * **Example 2:**
 *
 * **Input:** nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
 *
 * **Output:** 3
 *
 * **Example 3:**
 *
 * **Input:** nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
 *
 * **Output:** 2
 *
 * **Constraints:**
 *
 * *   `1 <= nums1.length, nums2.length <= 500`
 * *   `1 <= nums1[i], nums2[j] <= 2000`
**/
public class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[] dp = new int[nums2.length + 1];
        for (int i = 1; i <= nums1.length; i++) {
            int[] dpRow = new int[nums2.length + 1];
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dpRow[j] = dp[j - 1] + 1;
                } else {
                    dpRow[j] = Math.max(dp[j], dpRow[j - 1]);
                }
            }
            dp = dpRow;
        }

        return dp[nums2.length];
    }
}