g1201_1300.s1266_minimum_time_visiting_all_points.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g1201_1300.s1266_minimum_time_visiting_all_points;

// #Easy #Array #Math #Geometry #2022_03_14_Time_1_ms_(80.97%)_Space_43.8_MB_(26.31%)

/**
 * 1266 - Minimum Time Visiting All Points\.
 *
 * Easy
 *
 * On a 2D plane, there are `n` points with integer coordinates points[i] = [x_i, y_i]. Return _the **minimum time** in seconds to visit all the points in the order given by_ `points`.
 *
 * You can move according to these rules:
 *
 * *   In `1` second, you can either:
 *     *   move vertically by one unit,
 *     *   move horizontally by one unit, or
 *     *   move diagonally `sqrt(2)` units (in other words, move one unit vertically then one unit horizontally in `1` second).
 * *   You have to visit the points in the same order as they appear in the array.
 * *   You are allowed to pass through points that appear later in the order, but these do not count as visits.
 *
 * **Example 1:**
 *
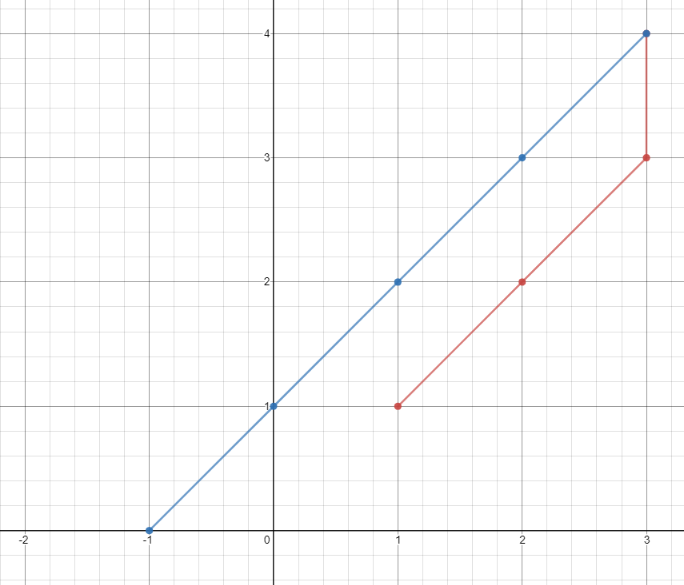
 * ![](https://assets.leetcode.com/uploads/2019/11/14/1626_example_1.PNG)
 *
 * **Input:** points = \[\[1,1],[3,4],[-1,0]]
 *
 * **Output:** 7
 *
 * **Explanation:** One optimal path is **[1,1]** -> [2,2] -> [3,3] -> **[3,4]** \-> [2,3] -> [1,2] -> [0,1] -> **[-1,0]** 
 *
 * Time from [1,1] to [3,4] = 3 seconds 
 *
 * Time from [3,4] to [-1,0] = 4 seconds 
 *
 * Total time = 7 seconds
 *
 * **Example 2:**
 *
 * **Input:** points = \[\[3,2],[-2,2]]
 *
 * **Output:** 5
 *
 * **Constraints:**
 *
 * *   `points.length == n`
 * *   `1 <= n <= 100`
 * *   `points[i].length == 2`
 * *   `-1000 <= points[i][0], points[i][1] <= 1000`
**/
public class Solution {
    public int minTimeToVisitAllPoints(int[][] points) {
        int minTime = 0;
        for (int i = 0; i < points.length - 1; i++) {
            minTime += chebyshevDistance(points[i], points[i + 1]);
        }
        return minTime;
    }

    private int chebyshevDistance(int[] pointA, int[] pointB) {
        return Math.max(Math.abs(pointA[0] - pointB[0]), Math.abs(pointA[1] - pointB[1]));
    }
}