g1301_1400.s1386_cinema_seat_allocation.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1301_1400.s1386_cinema_seat_allocation;

// #Medium #Array #Hash_Table #Greedy #Bit_Manipulation
// #2022_03_21_Time_32_ms_(69.41%)_Space_68.7_MB_(68.13%)

import java.util.HashMap;
import java.util.Map;

/**
 * 1386 - Cinema Seat Allocation\.
 *
 * Medium
 *
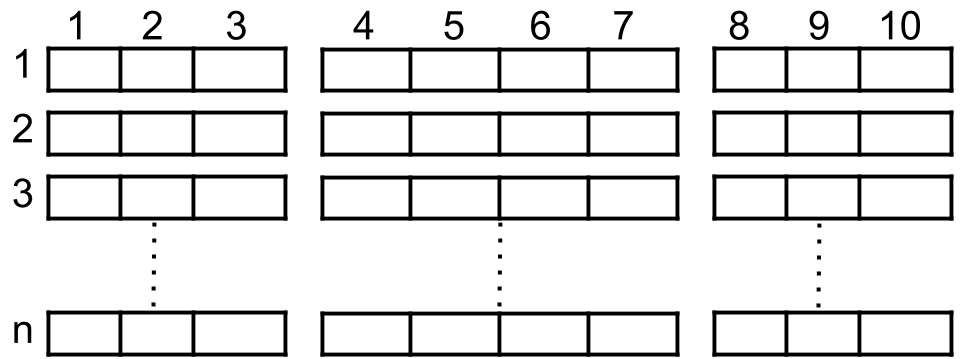
 * ![](https://assets.leetcode.com/uploads/2020/02/14/cinema_seats_1.png)
 *
 * A cinema has `n` rows of seats, numbered from 1 to `n` and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
 *
 * Given the array `reservedSeats` containing the numbers of seats already reserved, for example, `reservedSeats[i] = [3,8]` means the seat located in row **3** and labelled with **8** is already reserved.
 *
 * _Return the maximum number of four-person groups you can assign on the cinema seats._ A four-person group occupies four adjacent seats **in one single row**. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
 *
 * **Example 1:**
 *
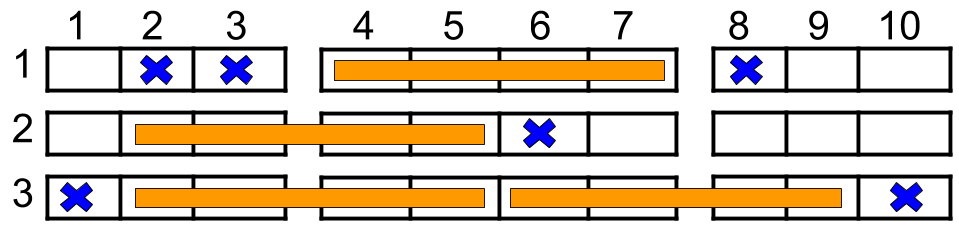
 * ![](https://assets.leetcode.com/uploads/2020/02/14/cinema_seats_3.png)
 *
 * **Input:** n = 3, reservedSeats = \[\[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
 *
 * **Output:** 4
 *
 * **Explanation:** The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
 *
 * **Example 2:**
 *
 * **Input:** n = 2, reservedSeats = \[\[2,1],[1,8],[2,6]]
 *
 * **Output:** 2
 *
 * **Example 3:**
 *
 * **Input:** n = 4, reservedSeats = \[\[4,3],[1,4],[4,6],[1,7]]
 *
 * **Output:** 4
 *
 * **Constraints:**
 *
 * *   `1 <= n <= 10^9`
 * *   `1 <= reservedSeats.length <= min(10*n, 10^4)`
 * *   `reservedSeats[i].length == 2`
 * *   `1 <= reservedSeats[i][0] <= n`
 * *   `1 <= reservedSeats[i][1] <= 10`
 * *   All `reservedSeats[i]` are distinct.
**/
public class Solution {
    public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
        Map occupiedFamilySeats = new HashMap<>();
        for (int[] reservedSeat : reservedSeats) {
            int row = reservedSeat[0];
            int col = reservedSeat[1];
            if (col == 1 || col == 10) {
                continue;
            }
            int[] rowFamilySeats = occupiedFamilySeats.getOrDefault(row, new int[3]);
            if (col == 2 || col == 3) {
                // mark left family seating as occupied
                rowFamilySeats[0] = 1;
                occupiedFamilySeats.put(row, rowFamilySeats);
            }
            if (col == 8 || col == 9) {
                // mark right family seating as occupied
                rowFamilySeats[2] = 1;
                occupiedFamilySeats.put(row, rowFamilySeats);
            }
            if (col == 4 || col == 5) {
                // mark left family seating as occupied
                rowFamilySeats[0] = 1;
                // mark min family seating as occupied
                rowFamilySeats[1] = 1;
                occupiedFamilySeats.put(row, rowFamilySeats);
            }
            if (col == 6 || col == 7) {
                // mark min family seating as occupied
                rowFamilySeats[1] = 1;
                // mark right family seating as occupied
                rowFamilySeats[2] = 1;
                occupiedFamilySeats.put(row, rowFamilySeats);
            }
        }
        // max number of family seats per row is 2, so we start that minus the rows for which we
        // have reservations
        int count = n * 2 - 2 * occupiedFamilySeats.size();
        // for each row with reservations, count remaining family seatings
        for (int[] familySeats : occupiedFamilySeats.values()) {
            if (familySeats[0] == 0) {
                count++;
            }
            if (familySeats[2] == 0) {
                count++;
            }
            if (familySeats[0] != 0 && familySeats[2] != 0 && familySeats[1] == 0) {
                count++;
            }
        }
        return count;
    }
}