g1401_1500.s1401_circle_and_rectangle_overlapping.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g1401_1500.s1401_circle_and_rectangle_overlapping;

// #Medium #Math #Geometry #2022_04_29_Time_0_ms_(100.00%)_Space_40.5_MB_(68.97%)

/**
 * 1401 - Circle and Rectangle Overlapping\.
 *
 * Medium
 *
 * You are given a circle represented as `(radius, xCenter, yCenter)` and an axis-aligned rectangle represented as `(x1, y1, x2, y2)`, where `(x1, y1)` are the coordinates of the bottom-left corner, and `(x2, y2)` are the coordinates of the top-right corner of the rectangle.
 *
 * Return `true` _if the circle and rectangle are overlapped otherwise return_ `false`. In other words, check if there is **any** point (x_i, y_i) that belongs to the circle and the rectangle at the same time.
 *
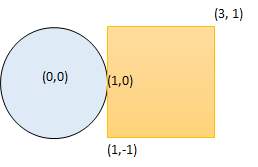
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/02/20/sample_4_1728.png)
 *
 * **Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
 *
 * **Output:** true
 *
 * **Explanation:** Circle and rectangle share the point (1,0).
 *
 * **Example 2:**
 *
 * **Input:** radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
 *
 * **Output:** false
 *
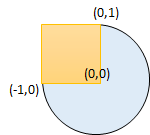
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/02/20/sample_2_1728.png)
 *
 * **Input:** radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
 *
 * **Output:** true
 *
 * **Constraints:**
 *
 * *   `1 <= radius <= 2000`
 * *   -10⁴ <= xCenter, yCenter <= 10⁴
 * *   -10⁴ <= x1 < x2 <= 10⁴
 * *   -10⁴ <= y1 < y2 <= 10⁴
**/
public class Solution {
    public boolean checkOverlap(
            int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {
        // Find the closest point to the circle within the rectangle
        int closestX = clamp(xCenter, x1, x2);
        int closestY = clamp(yCenter, y1, y2);
        // Calculate the distance between the circle's center and this closest point
        int distanceX = xCenter - closestX;
        int distanceY = yCenter - closestY;
        // If the distance is less than the circle's radius, an intersection occurs
        int distanceSquared = distanceX * distanceX + distanceY * distanceY;
        return distanceSquared <= radius * radius;
    }

    private int clamp(int val, int min, int max) {
        return Math.max(min, Math.min(max, val));
    }
}