g1401_1500.s1463_cherry_pickup_ii.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1401_1500.s1463_cherry_pickup_ii;

// #Hard #Array #Dynamic_Programming #Matrix #2022_03_29_Time_10_ms_(99.58%)_Space_43.1_MB_(83.50%)

/**
 * 1463 - Cherry Pickup II\.
 *
 * Hard
 *
 * You are given a `rows x cols` matrix `grid` representing a field of cherries where `grid[i][j]` represents the number of cherries that you can collect from the `(i, j)` cell.
 *
 * You have two robots that can collect cherries for you:
 *
 * *   **Robot #1** is located at the **top-left corner** `(0, 0)`, and
 * *   **Robot #2** is located at the **top-right corner** `(0, cols - 1)`.
 *
 * Return _the maximum number of cherries collection using both robots by following the rules below_:
 *
 * *   From a cell `(i, j)`, robots can move to cell `(i + 1, j - 1)`, `(i + 1, j)`, or `(i + 1, j + 1)`.
 * *   When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
 * *   When both robots stay in the same cell, only one takes the cherries.
 * *   Both robots cannot move outside of the grid at any moment.
 * *   Both robots should reach the bottom row in `grid`.
 *
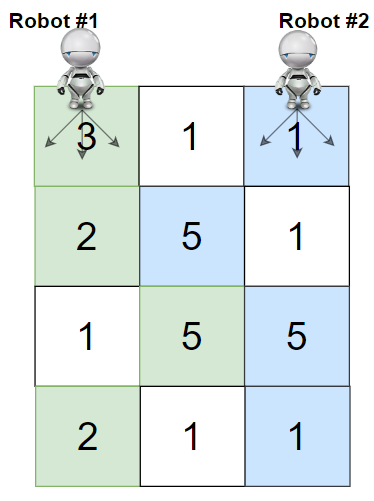
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/04/29/sample_1_1802.png)
 *
 * **Input:** grid = \[\[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
 *
 * **Output:** 24
 *
 * **Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
 *
 * Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
 *
 * Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12. 
 *
 * Total of cherries: 12 + 12 = 24.
 *
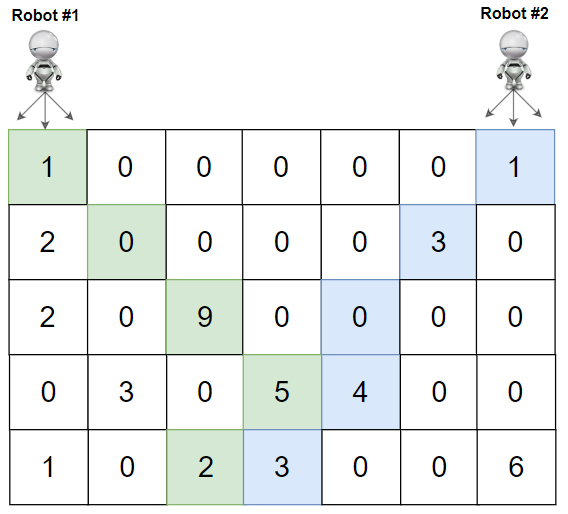
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/04/23/sample_2_1802.png)
 *
 * **Input:** grid = \[\[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
 *
 * **Output:** 28
 *
 * **Explanation:** Path of robot #1 and #2 are described in color green and blue respectively.
 *
 * Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
 *
 * Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11. 
 *
 * Total of cherries: 17 + 11 = 28.
 *
 * **Constraints:**
 *
 * *   `rows == grid.length`
 * *   `cols == grid[i].length`
 * *   `2 <= rows, cols <= 70`
 * *   `0 <= grid[i][j] <= 100`
**/
public class Solution {
    public int cherryPickup(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][][] dp = new int[n][n][m];
        dp[0][n - 1][0] = grid[0][0] + grid[0][n - 1];
        for (int k = 1; k < m; k++) {
            for (int i = 0; i <= Math.min(n - 1, k); i++) {
                for (int j = n - 1; j >= Math.max(0, n - 1 - k); j--) {
                    dp[i][j][k] = maxOfLast(dp, i, j, k) + grid[k][i] + ((i == j) ? 0 : grid[k][j]);
                }
            }
        }
        int result = 0;
        for (int i = 0; i <= Math.min(n - 1, m); i++) {
            for (int j = n - 1; j >= Math.max(0, n - 1 - m); j--) {
                result = Math.max(result, dp[i][j][m - 1]);
            }
        }
        return result;
    }

    private int maxOfLast(int[][][] dp, int i, int j, int k) {
        int result = 0;
        for (int x = -1; x <= 1; x++) {
            for (int y = -1; y <= 1; y++) {
                int r = i + x;
                int c = j + y;
                if (r >= 0 && r < dp[0].length && c >= 0 && c < dp[0].length) {
                    result = Math.max(result, dp[r][c][k - 1]);
                }
            }
        }
        return result;
    }
}