g1501_1600.s1514_path_with_maximum_probability.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1501_1600.s1514_path_with_maximum_probability;

// #Medium #Heap_Priority_Queue #Graph #Shortest_Path
// #2022_04_09_Time_31_ms_(93.10%)_Space_51.7_MB_(98.80%)

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

/**
 * 1514 - Path with Maximum Probability\.
 *
 * Medium
 *
 * You are given an undirected weighted graph of `n` nodes (0-indexed), represented by an edge list where `edges[i] = [a, b]` is an undirected edge connecting the nodes `a` and `b` with a probability of success of traversing that edge `succProb[i]`.
 *
 * Given two nodes `start` and `end`, find the path with the maximum probability of success to go from `start` to `end` and return its success probability.
 *
 * If there is no path from `start` to `end`, **return 0**. Your answer will be accepted if it differs from the correct answer by at most **1e-5**.
 *
 * **Example 1:**
 *
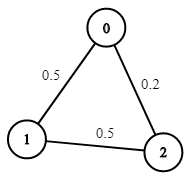 * **![](https://assets.leetcode.com/uploads/2019/09/20/1558_ex1.png)**
 *
 * **Input:** n = 3, edges = \[\[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
 *
 * **Output:** 0.25000
 *
 * **Explanation:** There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 \* 0.5 = 0.25.
 *
 * **Example 2:**
 *
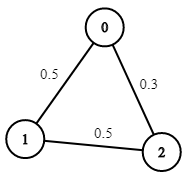 * **![](https://assets.leetcode.com/uploads/2019/09/20/1558_ex2.png)**
 *
 * **Input:** n = 3, edges = \[\[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
 *
 * **Output:** 0.30000
 *
 * **Example 3:**
 *
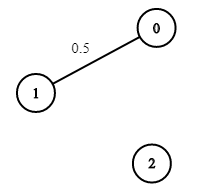 * **![](https://assets.leetcode.com/uploads/2019/09/20/1558_ex3.png)**
 *
 * **Input:** n = 3, edges = \[\[0,1]], succProb = [0.5], start = 0, end = 2
 *
 * **Output:** 0.00000
 *
 * **Explanation:** There is no path between 0 and 2.
 *
 * **Constraints:**
 *
 * *   `2 <= n <= 10^4`
 * *   `0 <= start, end < n`
 * *   `start != end`
 * *   `0 <= a, b < n`
 * *   `a != b`
 * *   `0 <= succProb.length == edges.length <= 2*10^4`
 * *   `0 <= succProb[i] <= 1`
 * *   There is at most one edge between every two nodes.
**/
@SuppressWarnings("unchecked")
public class Solution {
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        List[] nodeToNodesList = new List[n];
        List[] nodeToProbabilitiesList = new List[n];
        for (int i = 0; i < n; i++) {
            nodeToNodesList[i] = new ArrayList<>();
            nodeToProbabilitiesList[i] = new ArrayList<>();
        }
        for (int i = 0; i < edges.length; i++) {
            int u = edges[i][0];
            int v = edges[i][1];
            double w = succProb[i];
            nodeToNodesList[u].add(v);
            nodeToProbabilitiesList[u].add(w);
            nodeToNodesList[v].add(u);
            nodeToProbabilitiesList[v].add(w);
        }
        double[] probabilities = new double[n];
        probabilities[start] = 1.0;
        boolean[] visited = new boolean[n];
        Queue queue = new ArrayDeque<>();
        queue.add(start);
        visited[start] = true;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            visited[u] = false;
            for (int i = 0; i < nodeToNodesList[u].size(); i++) {
                int v = nodeToNodesList[u].get(i);
                double w = nodeToProbabilitiesList[u].get(i);
                if (probabilities[u] * w > probabilities[v]) {
                    probabilities[v] = probabilities[u] * w;
                    if (!visited[v]) {
                        visited[v] = true;
                        queue.add(v);
                    }
                }
            }
        }
        return probabilities[end];
    }
}