g1601_1700.s1627_graph_connectivity_with_threshold.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1601_1700.s1627_graph_connectivity_with_threshold;

// #Hard #Array #Math #Union_Find #2022_04_18_Time_7_ms_(98.45%)_Space_75.7_MB_(97.93%)

import java.util.ArrayList;
import java.util.List;

/**
 * 1627 - Graph Connectivity With Threshold\.
 *
 * Hard
 *
 * We have `n` cities labeled from `1` to `n`. Two different cities with labels `x` and `y` are directly connected by a bidirectional road if and only if `x` and `y` share a common divisor **strictly greater** than some `threshold`. More formally, cities with labels `x` and `y` have a road between them if there exists an integer `z` such that all of the following are true:
 *
 * *   `x % z == 0`,
 * *   `y % z == 0`, and
 * *   `z > threshold`.
 *
 * Given the two integers, `n` and `threshold`, and an array of `queries`, you must determine for each queries[i] = [a_i, b_i] if cities a_i and b_i are connected directly or indirectly. (i.e. there is some path between them).
 *
 * Return _an array_ `answer`_, where_ `answer.length == queries.length` _and_ `answer[i]` _is_ `true` _if for the_ i^th _query, there is a path between_ a_i _and_ b_i_, or_ `answer[i]` _is_ `false` _if there is no path._
 *
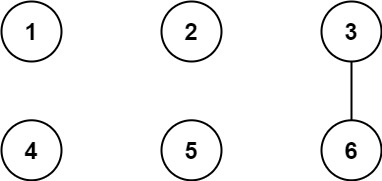
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/10/09/ex1.jpg)
 *
 * **Input:** n = 6, threshold = 2, queries = \[\[1,4],[2,5],[3,6]]
 *
 * **Output:** [false,false,true]
 *
 * **Explanation:** The divisors for each number: 
 *
 * 1: 1 
 *
 * 2: 1, 2 
 *
 * 3: 1, 3 
 *
 * 4: 1, 2, 4 
 *
 * 5: 1, 5 
 *
 * 6: 1, 2, 3, 6 
 *
 * Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the only ones directly connected. The result of each query: 
 *
 * [1,4] 1 is not connected to 4 
 *
 * [2,5] 2 is not connected to 5 
 *
 * [3,6] 3 is connected to 6 through path 3--6
 *
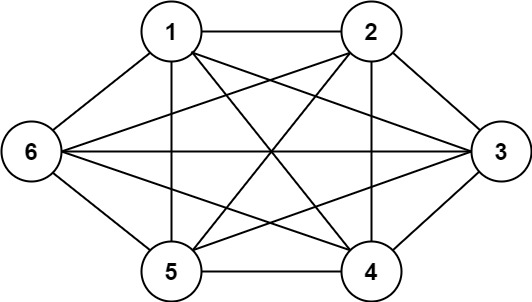
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/10/10/tmp.jpg)
 *
 * **Input:** n = 6, threshold = 0, queries = \[\[4,5],[3,4],[3,2],[2,6],[1,3]]
 *
 * **Output:** [true,true,true,true,true]
 *
 * **Explanation:** The divisors for each number are the same as the previous example. However, since the threshold is 0, all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.
 *
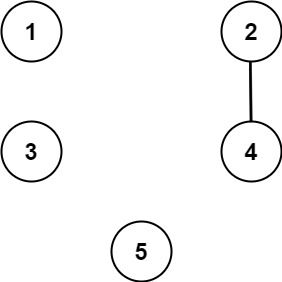
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/10/17/ex3.jpg)
 *
 * **Input:** n = 5, threshold = 1, queries = \[\[4,5],[4,5],[3,2],[2,3],[3,4]]
 *
 * **Output:** [false,false,false,false,false]
 *
 * **Explanation:** Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected. Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].
 *
 * **Constraints:**
 *
 * *   2 <= n <= 10⁴
 * *   `0 <= threshold <= n`
 * *   1 <= queries.length <= 10⁵
 * *   `queries[i].length == 2`
 * *   1 <= a_i, b_i <= cities
 * *   a_i != b_i
**/
public class Solution {
    public List areConnected(int n, int threshold, int[][] queries) {
        if (n < 1 || queries == null || queries.length == 0) {
            return new ArrayList<>();
        }
        int i;
        int j;
        int k;
        int x;
        DisjointSetUnion set = new DisjointSetUnion(n + 1);
        int edges = queries.length;
        for (i = threshold + 1; i <= n; i++) {
            k = n / i;
            x = i;
            for (j = 2; j <= k; j++) {
                x = x + i;
                set.union(i, x);
            }
        }
        List result = new ArrayList<>(edges);
        for (int[] query : queries) {
            result.add(set.find(query[0]) == set.find(query[1]));
        }
        return result;
    }

    private static class DisjointSetUnion {
        private final int[] rank;
        private final int[] parent;

        public DisjointSetUnion(int n) {
            rank = new int[n];
            parent = new int[n];
            for (int i = 0; i < n; i++) {
                this.rank[i] = 1;
                this.parent[i] = i;
            }
        }

        public int find(int u) {
            int x = u;
            while (x != parent[x]) {
                x = parent[x];
            }
            parent[u] = x;
            return x;
        }

        public void union(int u, int v) {
            if (u != v) {
                int x = find(u);
                int y = find(v);
                if (x != y) {
                    if (rank[x] > rank[y]) {
                        rank[x] += rank[y];
                        parent[y] = x;
                    } else {
                        rank[y] += rank[x];
                        parent[x] = y;
                    }
                }
            }
        }
    }
}