g1601_1700.s1659_maximize_grid_happiness.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1601_1700.s1659_maximize_grid_happiness;

// #Hard #Dynamic_Programming #Bit_Manipulation #Bitmask #Memoization
// #2022_04_23_Time_95_ms_(75.00%)_Space_53.1_MB_(58.33%)

/**
 * 1659 - Maximize Grid Happiness\.
 *
 * Hard
 *
 * You are given four integers, `m`, `n`, `introvertsCount`, and `extrovertsCount`. You have an `m x n` grid, and there are two types of people: introverts and extroverts. There are `introvertsCount` introverts and `extrovertsCount` extroverts.
 *
 * You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you **do not** have to have all the people living in the grid.
 *
 * The **happiness** of each person is calculated as follows:
 *
 * *   Introverts **start** with `120` happiness and **lose** `30` happiness for each neighbor (introvert or extrovert).
 * *   Extroverts **start** with `40` happiness and **gain** `20` happiness for each neighbor (introvert or extrovert).
 *
 * Neighbors live in the directly adjacent cells north, east, south, and west of a person's cell.
 *
 * The **grid happiness** is the **sum** of each person's happiness. Return _the **maximum possible grid happiness**._
 *
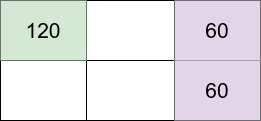
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2020/11/05/grid_happiness.png)
 *
 * **Input:** m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
 *
 * **Output:** 240
 *
 * **Explanation:** Assume the grid is 1-indexed with coordinates (row, column).
 *
 * We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
 *
 * - Introvert at (1,1) happiness: 120 (starting happiness) - (0 \* 30) (0 neighbors) = 120
 *
 * - Extrovert at (1,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
 *
 * - Extrovert at (2,3) happiness: 40 (starting happiness) + (1 \* 20) (1 neighbor) = 60
 *
 * The grid happiness is 120 + 60 + 60 = 240.
 *
 * The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.
 *
 * **Example 2:**
 *
 * **Input:** m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
 *
 * **Output:** 260
 *
 * **Explanation:** Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
 *
 * - Introvert at (1,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
 *
 * - Extrovert at (2,1) happiness: 40 (starting happiness) + (2 \* 20) (2 neighbors) = 80
 *
 * - Introvert at (3,1) happiness: 120 (starting happiness) - (1 \* 30) (1 neighbor) = 90
 *
 * The grid happiness is 90 + 80 + 90 = 260.
 *
 * **Example 3:**
 *
 * **Input:** m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
 *
 * **Output:** 240
 *
 * **Constraints:**
 *
 * *   `1 <= m, n <= 5`
 * *   `0 <= introvertsCount, extrovertsCount <= min(m * n, 6)`
**/
public class Solution {
    private int m;
    private int n;
    private int[][][][][] dp;
    private int notPlace = 0;
    private int intro = 1;
    private int extro = 2;
    private int mod;

    public int getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount) {
        this.m = m;
        this.n = n;
        int numOfState = (int) Math.pow(3, n);
        this.dp = new int[m][n][introvertsCount + 1][extrovertsCount + 1][numOfState];
        this.mod = numOfState / 3;
        return dfs(0, 0, introvertsCount, extrovertsCount, 0);
    }

    private int dfs(int x, int y, int ic, int ec, int state) {
        if (x == m) {
            return 0;
        } else if (y == n) {
            return dfs(x + 1, 0, ic, ec, state);
        }
        if (dp[x][y][ic][ec][state] != 0) {
            return dp[x][y][ic][ec][state];
        }
        // 1 - not place
        int max = dfs(x, y + 1, ic, ec, (state % mod) * 3);
        int up = state / mod;
        int left = state % 3;
        // 2 - place intro
        if (ic > 0) {
            int temp = 120;
            if (x > 0 && up != notPlace) {
                temp -= 30;
                temp += up == intro ? -30 : 20;
            }
            if (y > 0 && left != notPlace) {
                temp -= 30;
                temp += left == intro ? -30 : 20;
            }
            int nextState = state;
            nextState %= mod;
            nextState *= 3;
            nextState += intro;
            max = Math.max(max, temp + dfs(x, y + 1, ic - 1, ec, nextState));
        }
        // 3 - place extro
        if (ec > 0) {
            int temp = 40;
            if (x > 0 && up != notPlace) {
                temp += 20;
                temp += up == intro ? -30 : 20;
            }
            if (y > 0 && left != notPlace) {
                temp += 20;
                temp += left == intro ? -30 : 20;
            }
            int nextState = state;
            nextState %= mod;
            nextState *= 3;
            nextState += extro;
            max = Math.max(max, temp + dfs(x, y + 1, ic, ec - 1, nextState));
        }
        dp[x][y][ic][ec][state] = max;
        return max;
    }
}