g1701_1800.s1739_building_boxes.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1701_1800.s1739_building_boxes;

// #Hard #Math #Greedy #Binary_Search #2022_04_29_Time_1_ms_(84.38%)_Space_39.2_MB_(84.38%)

/**
 * 1739 - Building Boxes\.
 *
 * Hard
 *
 * You have a cubic storeroom where the width, length, and height of the room are all equal to `n` units. You are asked to place `n` boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:
 *
 * *   You can place the boxes anywhere on the floor.
 * *   If box `x` is placed on top of the box `y`, then each side of the four vertical sides of the box `y` **must** either be adjacent to another box or to a wall.
 *
 * Given an integer `n`, return _the **minimum** possible number of boxes touching the floor._
 *
 * **Example 1:**
 *
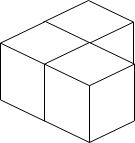
 * ![](https://assets.leetcode.com/uploads/2021/01/04/3-boxes.png)
 *
 * **Input:** n = 3
 *
 * **Output:** 3
 *
 * **Explanation:** The figure above is for the placement of the three boxes. These boxes are placed in the corner of the room, where the corner is on the left side.
 *
 * **Example 2:**
 *
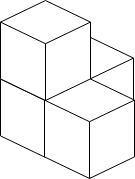
 * ![](https://assets.leetcode.com/uploads/2021/01/04/4-boxes.png)
 *
 * **Input:** n = 4
 *
 * **Output:** 3
 *
 * **Explanation:** The figure above is for the placement of the four boxes. These boxes are placed in the corner of the room, where the corner is on the left side.
 *
 * **Example 3:**
 *
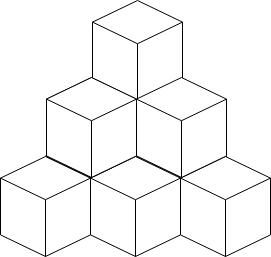
 * ![](https://assets.leetcode.com/uploads/2021/01/04/10-boxes.png)
 *
 * **Input:** n = 10
 *
 * **Output:** 6
 *
 * **Explanation:** The figure above is for the placement of the ten boxes. These boxes are placed in the corner of the room, where the corner is on the back side.
 *
 * **Constraints:**
 *
 * *   1 <= n <= 10⁹
**/
public class Solution {
    static final double ONE_THIRD = 1.0d / 3.0d;

    public int minimumBoxes(int n) {
        int k = findLargestTetrahedralNotGreaterThan(n);
        int used = tetrahedral(k);
        int floor = triangular(k);
        int unused = (n - used);
        if (unused == 0) {
            return floor;
        }
        int r = findSmallestTriangularNotLessThan(unused);
        return (floor + r);
    }

    private int findLargestTetrahedralNotGreaterThan(int te) {
        int a = (int) Math.ceil(Math.pow(product(6, te), ONE_THIRD));
        while (tetrahedral(a) > te) {
            a--;
        }
        return a;
    }

    private int findSmallestTriangularNotLessThan(int t) {
        int a = -1 + (int) Math.floor(Math.sqrt(product(t, 2)));
        while (triangular(a) < t) {
            a++;
        }
        return a;
    }

    private int tetrahedral(int a) {
        return (int) ratio(product(a, a + 1, a + 2), 6);
    }

    private int triangular(int a) {
        return (int) ratio(product(a, a + 1), 2);
    }

    private long product(long... vals) {
        long product = 1L;
        for (long val : vals) {
            product *= val;
        }
        return product;
    }

    private long ratio(long a, long b) {
        return (a / b);
    }
}