g1701_1800.s1765_map_of_highest_peak.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1701_1800.s1765_map_of_highest_peak;

// #Medium #Array #Breadth_First_Search #Matrix
// #2022_04_30_Time_64_ms_(85.40%)_Space_139.8_MB_(98.14%)

import java.util.LinkedList;
import java.util.Queue;

/**
 * 1765 - Map of Highest Peak\.
 *
 * Medium
 *
 * You are given an integer matrix `isWater` of size `m x n` that represents a map of **land** and **water** cells.
 *
 * *   If `isWater[i][j] == 0`, cell `(i, j)` is a **land** cell.
 * *   If `isWater[i][j] == 1`, cell `(i, j)` is a **water** cell.
 *
 * You must assign each cell a height in a way that follows these rules:
 *
 * *   The height of each cell must be non-negative.
 * *   If the cell is a **water** cell, its height must be `0`.
 * *   Any two adjacent cells must have an absolute height difference of **at most** `1`. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
 *
 * Find an assignment of heights such that the maximum height in the matrix is **maximized**.
 *
 * Return _an integer matrix_ `height` _of size_ `m x n` _where_ `height[i][j]` _is cell_ `(i, j)`_'s height. If there are multiple solutions, return **any** of them_.
 *
 * **Example 1:**
 *
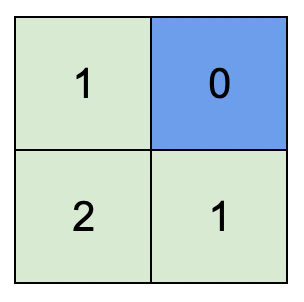 * **![](https://assets.leetcode.com/uploads/2021/01/10/screenshot-2021-01-11-at-82045-am.png)**
 *
 * **Input:** isWater = \[\[0,1],[0,0]]
 *
 * **Output:** [[1,0],[2,1]]
 *
 * **Explanation:** The image shows the assigned heights of each cell. The blue cell is the water cell, and the green cells are the land cells.
 *
 * **Example 2:**
 *
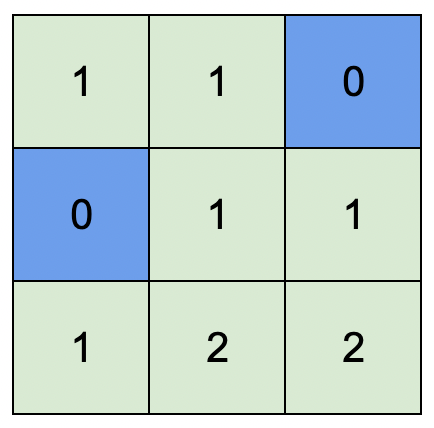 * **![](https://assets.leetcode.com/uploads/2021/01/10/screenshot-2021-01-11-at-82050-am.png)**
 *
 * **Input:** isWater = \[\[0,0,1],[1,0,0],[0,0,0]]
 *
 * **Output:** [[1,1,0],[0,1,1],[1,2,2]]
 *
 * **Explanation:** A height of 2 is the maximum possible height of any assignment. Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.
 *
 * **Constraints:**
 *
 * *   `m == isWater.length`
 * *   `n == isWater[i].length`
 * *   `1 <= m, n <= 1000`
 * *   `isWater[i][j]` is `0` or `1`.
 * *   There is at least **one** water cell.
**/
public class Solution {
    private final int[] dir = {0, 1, 0, -1, 0};

    public int[][] highestPeak(int[][] isWater) {
        int h = 1;
        Queue q = new LinkedList<>();
        for (int i = 0; i < isWater.length; i++) {
            for (int j = 0; j < isWater[0].length; j++) {
                isWater[i][j] = isWater[i][j] == 1 ? 0 : -1;
                if (isWater[i][j] == 0) {
                    q.add(new int[] {i, j});
                }
            }
        }
        while (!q.isEmpty()) {
            Queue q1 = new LinkedList<>();
            for (int[] cur : q) {
                int x = cur[0];
                int y = cur[1];
                for (int i = 0; i < 4; i++) {
                    int nx = x + dir[i];
                    int ny = y + dir[i + 1];
                    if (nx >= 0
                            && nx < isWater.length
                            && ny >= 0
                            && ny < isWater[0].length
                            && isWater[nx][ny] == -1) {
                        isWater[nx][ny] = h;
                        q1.add(new int[] {nx, ny});
                    }
                }
            }
            h++;
            q = q1;
        }
        return isWater;
    }
}