g1701_1800.s1766_tree_of_coprimes.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1701_1800.s1766_tree_of_coprimes;

// #Hard #Math #Depth_First_Search #Breadth_First_Search #Tree
// #2022_04_30_Time_111_ms_(94.07%)_Space_155.4_MB_(40.68%)

import java.util.ArrayList;
import java.util.Arrays;

/**
 * 1766 - Tree of Coprimes\.
 *
 * Hard
 *
 * There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of `n` nodes numbered from `0` to `n - 1` and exactly `n - 1` edges. Each node has a value associated with it, and the **root** of the tree is node `0`.
 *
 * To represent this tree, you are given an integer array `nums` and a 2D array `edges`. Each `nums[i]` represents the i^th node's value, and each edges[j] = [u_j, v_j] represents an edge between nodes u_j and v_j in the tree.
 *
 * Two values `x` and `y` are **coprime** if `gcd(x, y) == 1` where `gcd(x, y)` is the **greatest common divisor** of `x` and `y`.
 *
 * An ancestor of a node `i` is any other node on the shortest path from node `i` to the **root**. A node is **not** considered an ancestor of itself.
 *
 * Return _an array_ `ans` _of size_ `n`, _where_ `ans[i]` _is the closest ancestor to node_ `i` _such that_ `nums[i]` _and_ `nums[ans[i]]` are **coprime** , or `-1` _if there is no such ancestor_.
 *
 * **Example 1:**
 *
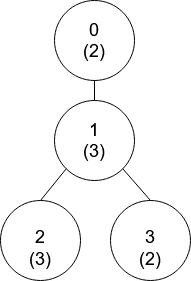
 * **![](https://assets.leetcode.com/uploads/2021/01/06/untitled-diagram.png)**
 *
 * **Input:** nums = [2,3,3,2], edges = \[\[0,1],[1,2],[1,3]]
 *
 * **Output:** [-1,0,0,1]
 *
 * **Explanation:** In the above figure, each node's value is in parentheses. 
 *
 * - Node 0 has no coprime ancestors. 
 *
 * - Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1). - Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor. 
 *
 * - Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its closest valid ancestor.
 *
 * **Example 2:**
 *
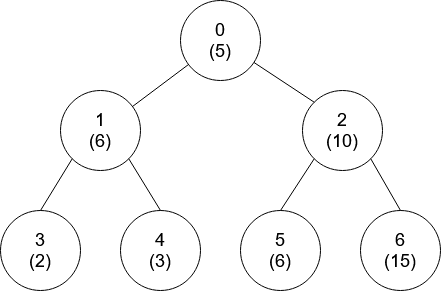
 * ![](https://assets.leetcode.com/uploads/2021/01/06/untitled-diagram1.png)
 *
 * **Input:** nums = [5,6,10,2,3,6,15], edges = \[\[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
 *
 * **Output:** [-1,0,-1,0,0,0,-1]
 *
 * **Constraints:**
 *
 * *   `nums.length == n`
 * *   `1 <= nums[i] <= 50`
 * *   1 <= n <= 10⁵
 * *   `edges.length == n - 1`
 * *   `edges[j].length == 2`
 * *   0 <= u_j, v_j < n
 * *   u_j != v_j
**/
@SuppressWarnings({"unchecked", "java:S107"})
public class Solution {
    private void dfs(
            int[] v2n,
            int[] v2d,
            int depth,
            int parent,
            int node,
            int[] ans,
            int[] nums,
            ArrayList[] neighbors) {
        int d = Integer.MIN_VALUE;
        int n = -1;
        int v = nums[node];
        for (int i = 1; i <= 50; i++) {
            if (v2n[i] != -1 && v2d[i] > d && gcd(i, v) == 1) {
                d = v2d[i];
                n = v2n[i];
            }
        }
        ans[node] = n;
        int v2NOld = v2n[v];
        int v2DOld = v2d[v];
        v2n[v] = node;
        v2d[v] = depth;
        for (int child : neighbors[node]) {
            if (child == parent) {
                continue;
            }
            dfs(v2n, v2d, depth + 1, node, child, ans, nums, neighbors);
        }
        v2n[v] = v2NOld;
        v2d[v] = v2DOld;
    }

    private int gcd(int x, int y) {
        return x == 0 ? y : gcd(y % x, x);
    }

    public int[] getCoprimes(int[] nums, int[][] edges) {
        int n = nums.length;
        ArrayList[] neighbors = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            neighbors[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            neighbors[edge[0]].add(edge[1]);
            neighbors[edge[1]].add(edge[0]);
        }
        int[] ans = new int[n];
        int[] v2n = new int[51];
        int[] v2d = new int[51];
        Arrays.fill(v2n, -1);
        dfs(v2n, v2d, 0, -1, 0, ans, nums, neighbors);
        return ans;
    }
}