g1801_1900.s1819_number_of_different_subsequences_gcds.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g1801_1900.s1819_number_of_different_subsequences_gcds;

// #Hard #Array #Math #Counting #Number_Theory
// #2022_05_03_Time_116_ms_(96.43%)_Space_51.1_MB_(100.00%)

/**
 * 1819 - Number of Different Subsequences GCDs\.
 *
 * Hard
 *
 * You are given an array `nums` that consists of positive integers.
 *
 * The **GCD** of a sequence of numbers is defined as the greatest integer that divides **all** the numbers in the sequence evenly.
 *
 * *   For example, the GCD of the sequence `[4,6,16]` is `2`.
 *
 * A **subsequence** of an array is a sequence that can be formed by removing some elements (possibly none) of the array.
 *
 * *   For example, `[2,5,10]` is a subsequence of `[1,2,1, **2** ,4,1, **5** , **10** ]`.
 *
 * Return _the **number** of **different** GCDs among all **non-empty** subsequences of_ `nums`.
 *
 * **Example 1:**
 *
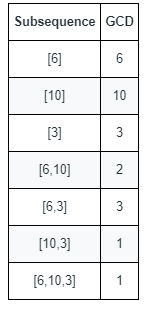
 * ![](https://assets.leetcode.com/uploads/2021/03/17/image-1.png)
 *
 * **Input:** nums = [6,10,3]
 *
 * **Output:** 5
 *
 * **Explanation:** The figure shows all the non-empty subsequences and their GCDs. The different GCDs are 6, 10, 3, 2, and 1.
 *
 * **Example 2:**
 *
 * **Input:** nums = [5,15,40,5,6]
 *
 * **Output:** 7
 *
 * **Constraints:**
 *
 * *   1 <= nums.length <= 10⁵
 * *   1 <= nums[i] <= 2 * 10⁵
**/
public class Solution {
    public int countDifferentSubsequenceGCDs(int[] nums) {
        int max = 0;
        for (int num : nums) {
            max = Math.max(max, num);
        }
        boolean[] present = new boolean[200001];
        for (int num : nums) {
            max = Math.max(max, num);
            present[num] = true;
        }
        int count = 0;
        for (int i = 1; i <= max; i++) {
            if (present[i]) {
                count++;
                continue;
            }
            int tempGcd = 0;
            for (int j = i; j <= max; j += i) {
                if (present[j]) {
                    tempGcd = gcd(tempGcd, j);
                }
                if (tempGcd == i) {
                    count++;
                    break;
                }
            }
        }
        return count;
    }

    private int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }
}