g1801_1900.s1824_minimum_sideway_jumps.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1801_1900.s1824_minimum_sideway_jumps;

// #Medium #Array #Dynamic_Programming #Greedy
// #2022_05_06_Time_17_ms_(96.34%)_Space_217.7_MB_(56.10%)

/**
 * 1824 - Minimum Sideway Jumps\.
 *
 * Medium
 *
 * There is a **3 lane road** of length `n` that consists of `n + 1` **points** labeled from `0` to `n`. A frog **starts** at point `0` in the **second** lane and wants to jump to point `n`. However, there could be obstacles along the way.
 *
 * You are given an array `obstacles` of length `n + 1` where each `obstacles[i]` ( **ranging from 0 to 3** ) describes an obstacle on the lane `obstacles[i]` at point `i`. If `obstacles[i] == 0`, there are no obstacles at point `i`. There will be **at most one** obstacle in the 3 lanes at each point.
 *
 * *   For example, if `obstacles[2] == 1`, then there is an obstacle on lane 1 at point 2.
 *
 * The frog can only travel from point `i` to point `i + 1` on the same lane if there is not an obstacle on the lane at point `i + 1`. To avoid obstacles, the frog can also perform a **side jump** to jump to **another** lane (even if they are not adjacent) at the **same** point if there is no obstacle on the new lane.
 *
 * *   For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.
 *
 * Return _the **minimum number of side jumps** the frog needs to reach **any lane** at point n starting from lane `2` at point 0._
 *
 * **Note:** There will be no obstacles on points `0` and `n`.
 *
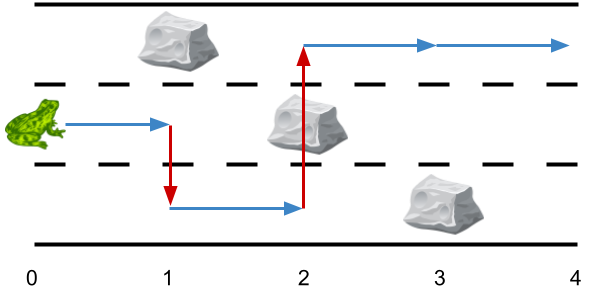
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/03/25/ic234-q3-ex1.png)
 *
 * **Input:** obstacles = [0,1,2,3,0]
 *
 * **Output:** 2
 *
 * **Explanation:** The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows). Note that the frog can jump over obstacles only when making side jumps (as shown at point 2). 
 *
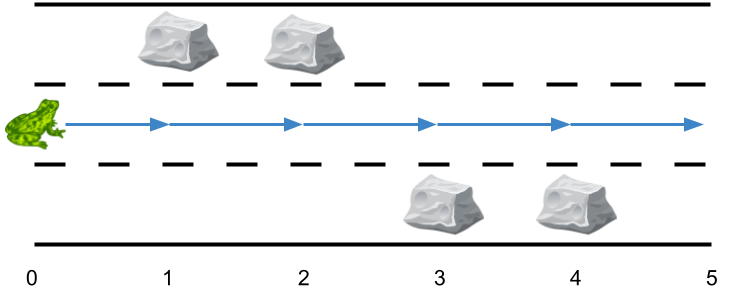
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/03/25/ic234-q3-ex2.png)
 *
 * **Input:** obstacles = [0,1,1,3,3,0]
 *
 * **Output:** 0
 *
 * **Explanation:** There are no obstacles on lane 2. No side jumps are required. 
 *
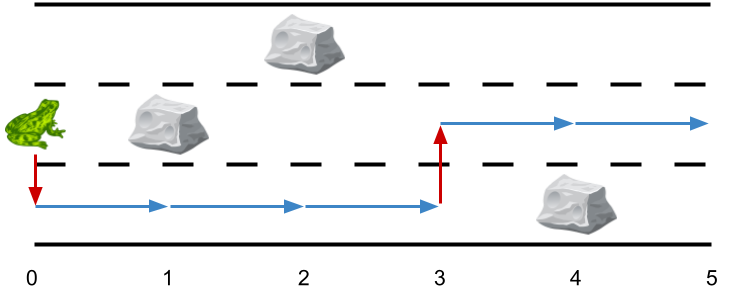
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/03/25/ic234-q3-ex3.png)
 *
 * **Input:** obstacles = [0,2,1,0,3,0]
 *
 * **Output:** 2
 *
 * **Explanation:** The optimal solution is shown by the arrows above. There are 2 side jumps. 
 *
 * **Constraints:**
 *
 * *   `obstacles.length == n + 1`
 * *   1 <= n <= 5 * 10⁵
 * *   `0 <= obstacles[i] <= 3`
 * *   `obstacles[0] == obstacles[n] == 0`
**/
public class Solution {
    public int minSideJumps(int[] obstacles) {
        int sideJumps = 0;
        int currLane = 2;
        int i = 0;
        while (i < obstacles.length - 1) {
            if (obstacles[i + 1] == currLane) {
                if (obstacles[i] != 0) {
                    currLane = getNextLane(obstacles[i], obstacles[i + 1]);
                } else {
                    int j = i + 2;
                    while (j < obstacles.length
                            && (obstacles[j] == 0 || obstacles[j] == obstacles[i + 1])) {
                        j++;
                    }
                    if (j < obstacles.length) {
                        currLane = getNextLane(obstacles[i + 1], obstacles[j]);
                    } else {
                        i = obstacles.length - 1;
                    }
                }
                sideJumps++;
            }
            i++;
        }
        return sideJumps;
    }

    private int getNextLane(int nextObstacle, int nextNextObstacle) {
        if ((nextObstacle == 2 && nextNextObstacle == 3)
                || (nextObstacle == 3 && nextNextObstacle == 2)) {
            return 1;
        }
        if ((nextObstacle == 1 && nextNextObstacle == 3)
                || (nextObstacle == 3 && nextNextObstacle == 1)) {
            return 2;
        } else {
            return 3;
        }
    }
}