g1801_1900.s1895_largest_magic_square.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1801_1900.s1895_largest_magic_square;

// #Medium #Array #Matrix #Prefix_Sum #2022_05_03_Time_7_ms_(80.72%)_Space_45.1_MB_(62.65%)

/**
 * 1895 - Largest Magic Square\.
 *
 * Medium
 *
 * A `k x k` **magic square** is a `k x k` grid filled with integers such that every row sum, every column sum, and both diagonal sums are **all equal**. The integers in the magic square **do not have to be distinct**. Every `1 x 1` grid is trivially a **magic square**.
 *
 * Given an `m x n` integer `grid`, return _the **size** (i.e., the side length_ `k`_) of the **largest magic square** that can be found within this grid_.
 *
 * **Example 1:**
 *
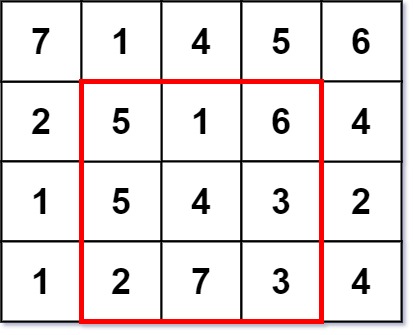
 * ![](https://assets.leetcode.com/uploads/2021/05/29/magicsquare-grid.jpg)
 *
 * **Input:** grid = \[\[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
 *
 * **Output:** 3
 *
 * **Explanation:** The largest magic square has a size of 3.
 *
 * Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
 *
 * - Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
 *
 * - Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
 *
 * - Diagonal sums: 5+4+3 = 6+4+2 = 12 
 *
 * **Example 2:**
 *
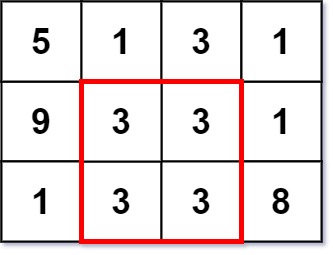
 * ![](https://assets.leetcode.com/uploads/2021/05/29/magicsquare2-grid.jpg)
 *
 * **Input:** grid = \[\[5,1,3,1],[9,3,3,1],[1,3,3,8]]
 *
 * **Output:** 2 
 *
 * **Constraints:**
 *
 * *   `m == grid.length`
 * *   `n == grid[i].length`
 * *   `1 <= m, n <= 50`
 * *   1 <= grid[i][j] <= 10⁶
**/
public class Solution {
    public int largestMagicSquare(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] rows = new int[m][n + 1];
        int[][] cols = new int[m + 1][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // cumulative sum for each row
                rows[i][j + 1] = rows[i][j] + grid[i][j];
                // cumulative sum for each column
                cols[i + 1][j] = cols[i][j] + grid[i][j];
            }
        }
        // start with the biggest side possible
        for (int side = Math.min(m, n); side > 1; side--) {
            // check every square
            for (int i = 0; i <= m - side; i++) {
                for (int j = 0; j <= n - side; j++) {
                    // checks if a square with top left [i, j] and side length is magic
                    if (magic(grid, rows, cols, i, j, side)) {
                        return side;
                    }
                }
            }
        }
        return 1;
    }

    private boolean magic(int[][] grid, int[][] rows, int[][] cols, int r, int c, int side) {
        int sum = rows[r][c + side] - rows[r][c];
        int d1 = 0;
        int d2 = 0;
        for (int k = 0; k < side; k++) {
            d1 += grid[r + k][c + k];
            d2 += grid[r + side - 1 - k][c + k];
            // check each row and column
            if (rows[r + k][c + side] - rows[r + k][c] != sum
                    || cols[r + side][c + k] - cols[r][c + k] != sum) {
                return false;
            }
        }
        // checks both diagonals
        return d1 == sum && d2 == sum;
    }
}