g1901_2000.s1901_find_a_peak_element_ii.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g1901_2000.s1901_find_a_peak_element_ii;

// #Medium #Array #Binary_Search #Matrix #Divide_and_Conquer #Binary_Search_II_Day_17
// #2022_05_11_Time_0_ms_(100.00%)_Space_115.1_MB_(45.96%)

/**
 * 1901 - Find a Peak Element II\.
 *
 * Medium
 *
 * A **peak** element in a 2D grid is an element that is **strictly greater** than all of its **adjacent** neighbors to the left, right, top, and bottom.
 *
 * Given a **0-indexed** `m x n` matrix `mat` where **no two adjacent cells are equal** , find **any** peak element `mat[i][j]` and return _the length 2 array_ `[i,j]`.
 *
 * You may assume that the entire matrix is surrounded by an **outer perimeter** with the value `-1` in each cell.
 *
 * You must write an algorithm that runs in `O(m log(n))` or `O(n log(m))` time.
 *
 * **Example 1:**
 *
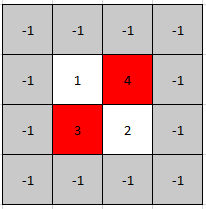
 * ![](https://assets.leetcode.com/uploads/2021/06/08/1.png)
 *
 * **Input:** mat = \[\[1,4],[3,2]]
 *
 * **Output:** [0,1]
 *
 * **Explanation:** Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.
 *
 * **Example 2:**
 *
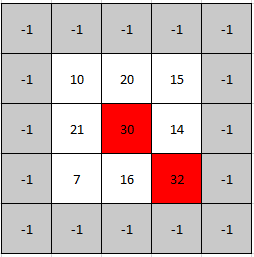
 * **![](https://assets.leetcode.com/uploads/2021/06/07/3.png)**
 *
 * **Input:** mat = \[\[10,20,15],[21,30,14],[7,16,32]]
 *
 * **Output:** [1,1]
 *
 * **Explanation:** Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.
 *
 * **Constraints:**
 *
 * *   `m == mat.length`
 * *   `n == mat[i].length`
 * *   `1 <= m, n <= 500`
 * *   1 <= mat[i][j] <= 10⁵
 * *   No two adjacent cells are equal.
**/
public class Solution {
    public int[] findPeakGrid(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        int l = 0;
        int r = m - 1;
        int mid;
        while (l <= r) {
            mid = (l + r) / 2;
            int mx = mat[0][mid];
            int mxi = 0;
            for (int i = 1; i < n; i++) {
                if (mx < mat[i][mid]) {
                    mx = mat[i][mid];
                    mxi = i;
                }
            }
            int lv = mid > l ? mat[mxi][mid - 1] : -1;
            int rv = mid < r ? mat[mxi][mid + 1] : -1;
            if (mx > lv && mx > rv) {
                return new int[] {mxi, mid};
            } else if (mx > lv) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return new int[] {-1, -1};
    }
}