g1901_2000.s1943_describe_the_painting.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1901_2000.s1943_describe_the_painting;

// #Medium #Array #Prefix_Sum #2022_05_16_Time_29_ms_(93.92%)_Space_127.4_MB_(75.00%)

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 1943 - Describe the Painting\.
 *
 * Medium
 *
 * There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where segments[i] = [start_i, end_i, color_i] represents the **half-closed segment** [start_i, end_i) with color_i as the color.
 *
 * The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
 *
 * *   For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
 *
 * For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
 *
 * You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where painting[j] = [left_j, right_j, mix_j] describes a **half-closed segment** [left_j, right_j) with the mixed color **sum** of mix_j.
 *
 * *   For example, the painting created with `segments = \[\[1,4,5],[1,7,7]]` can be described by `painting = \[\[1,4,12],[4,7,7]]` because:
 *     *   `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
 *     *   `[4,7)` is colored `{7}` from only the second segment.
 *
 * Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
 *
 * A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
 *
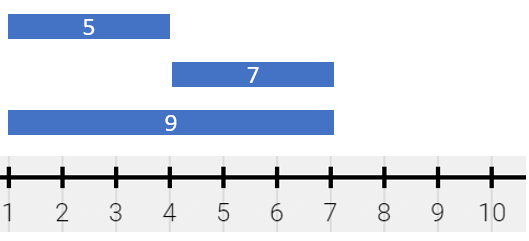
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/06/18/1.png)
 *
 * **Input:** segments = \[\[1,4,5],[4,7,7],[1,7,9]]
 *
 * **Output:** [[1,4,14],[4,7,16]]
 *
 * **Explanation:** The painting can be described as follows: 
 *
 * - [1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
 *
 * - [4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
 *
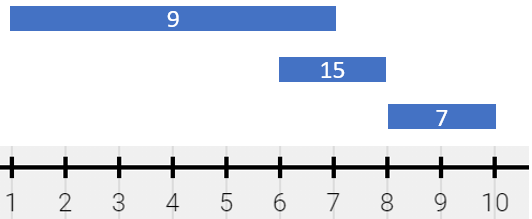
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/06/18/2.png)
 *
 * **Input:** segments = \[\[1,7,9],[6,8,15],[8,10,7]]
 *
 * **Output:** [[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
 *
 * **Explanation:** The painting can be described as follows: 
 *
 * - [1,6) is colored 9 from the first segment. 
 *
 * - [6,7) is colored {9,15} (with a sum of 24) from the first and second segments. 
 *
 * - [7,8) is colored 15 from the second segment. 
 *
 * - [8,10) is colored 7 from the third segment.
 *
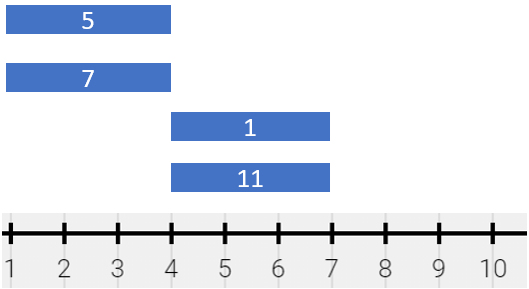
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/07/04/c1.png)
 *
 * **Input:** segments = \[\[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
 *
 * **Output:** [[1,4,12],[4,7,12]]
 *
 * **Explanation:** The painting can be described as follows:
 *
 * - [1,4) is colored {5,7} (with a sum of 12) from the first and second segments. 
 *
 * - [4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments. 
 *   
 * Note that returning a single segment [1,7) is incorrect because the mixed color sets are different.
 *
 * **Constraints:**
 *
 * *   1 <= segments.length <= 2 * 10⁴
 * *   `segments[i].length == 3`
 * *   1 <= start_i < end_i <= 10⁵
 * *   1 <= color_i <= 10⁹
 * *   Each color_i is distinct.
**/
public class Solution {
    public List> splitPainting(int[][] segments) {
        List> result = new ArrayList<>();
        int n = 1;
        for (int[] s : segments) {
            n = Math.max(n, s[1]);
        }
        n += 1;
        long[] line = new long[n];
        boolean[] endpoint = new boolean[n];
        for (int[] s : segments) {
            int start = s[0];
            int end = s[1];
            int color = s[2];
            line[start] += color;
            line[end] -= color;
            endpoint[start] = endpoint[end] = true;
        }
        long mixedColor = 0;
        int start = 1;
        for (int end = 1; end < n; end++) {
            if (endpoint[end]) {
                if (mixedColor > 0) {
                    result.add(Arrays.asList((long) start, (long) end, mixedColor));
                }
                start = end;
            }
            mixedColor += line[end];
        }
        return result;
    }
}