g1901_2000.s1975_maximum_matrix_sum.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g1901_2000.s1975_maximum_matrix_sum;

// #Medium #Array #Greedy #Matrix #2022_05_21_Time_4_ms_(100.00%)_Space_79.8_MB_(36.28%)

/**
 * 1975 - Maximum Matrix Sum\.
 *
 * Medium
 *
 * You are given an `n x n` integer `matrix`. You can do the following operation **any** number of times:
 *
 * *   Choose any two **adjacent** elements of `matrix` and **multiply** each of them by `-1`.
 *
 * Two elements are considered **adjacent** if and only if they share a **border**.
 *
 * Your goal is to **maximize** the summation of the matrix's elements. Return _the **maximum** sum of the matrix's elements using the operation mentioned above._
 *
 * **Example 1:**
 *
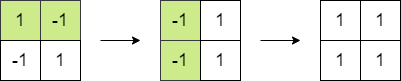
 * ![](https://assets.leetcode.com/uploads/2021/07/16/pc79-q2ex1.png)
 *
 * **Input:** matrix = \[\[1,-1],[-1,1]]
 *
 * **Output:** 4
 *
 * **Explanation:** We can follow the following steps to reach sum equals 4: 
 *
 * - Multiply the 2 elements in the first row by -1. 
 *
 * - Multiply the 2 elements in the first column by -1.
 *
 * **Example 2:**
 *
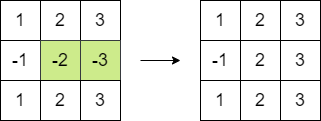
 * ![](https://assets.leetcode.com/uploads/2021/07/16/pc79-q2ex2.png)
 *
 * **Input:** matrix = \[\[1,2,3],[-1,-2,-3],[1,2,3]]
 *
 * **Output:** 16
 *
 * **Explanation:** We can follow the following step to reach sum equals 16: - Multiply the 2 last elements in the second row by -1.
 *
 * **Constraints:**
 *
 * *   `n == matrix.length == matrix[i].length`
 * *   `2 <= n <= 250`
 * *   -10⁵ <= matrix[i][j] <= 10⁵
**/
public class Solution {
    public long maxMatrixSum(int[][] matrix) {
        int numNegatives = 0;
        long totalSum = 0;
        int minNeg = Integer.MIN_VALUE;
        int minPos = Integer.MAX_VALUE;
        for (int[] ints : matrix) {
            for (int e = 0; e < matrix[0].length; e++) {
                int value = ints[e];
                if (value < 0) {
                    numNegatives++;
                    totalSum = totalSum - value;
                    minNeg = Math.max(value, minNeg);
                } else {
                    totalSum = totalSum + value;
                    minPos = Math.min(value, minPos);
                }
            }
        }

        int min = Math.min(minPos, -minNeg);

        return totalSum - numNegatives % 2 * (min + min);
    }
}