g1901_2000.s1992_find_all_groups_of_farmland.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g1901_2000.s1992_find_all_groups_of_farmland;

// #Medium #Array #Depth_First_Search #Breadth_First_Search #Matrix
// #2022_05_19_Time_7_ms_(89.08%)_Space_52.1_MB_(87.32%)

import java.util.ArrayList;
import java.util.List;

/**
 * 1992 - Find All Groups of Farmland\.
 *
 * Medium
 *
 * You are given a **0-indexed** `m x n` binary matrix `land` where a `0` represents a hectare of forested land and a `1` represents a hectare of farmland.
 *
 * To keep the land organized, there are designated rectangular areas of hectares that consist **entirely** of farmland. These rectangular areas are called **groups**. No two groups are adjacent, meaning farmland in one group is **not** four-directionally adjacent to another farmland in a different group.
 *
 * `land` can be represented by a coordinate system where the top left corner of `land` is `(0, 0)` and the bottom right corner of `land` is `(m-1, n-1)`. Find the coordinates of the top left and bottom right corner of each **group** of farmland. A **group** of farmland with a top left corner at (r₁, c₁) and a bottom right corner at (r₂, c₂) is represented by the 4-length array [r₁, c₁, r₂, c₂].
 *
 * Return _a 2D array containing the 4-length arrays described above for each **group** of farmland in_ `land`_. If there are no groups of farmland, return an empty array. You may return the answer in **any order**_.
 *
 * **Example 1:**
 *
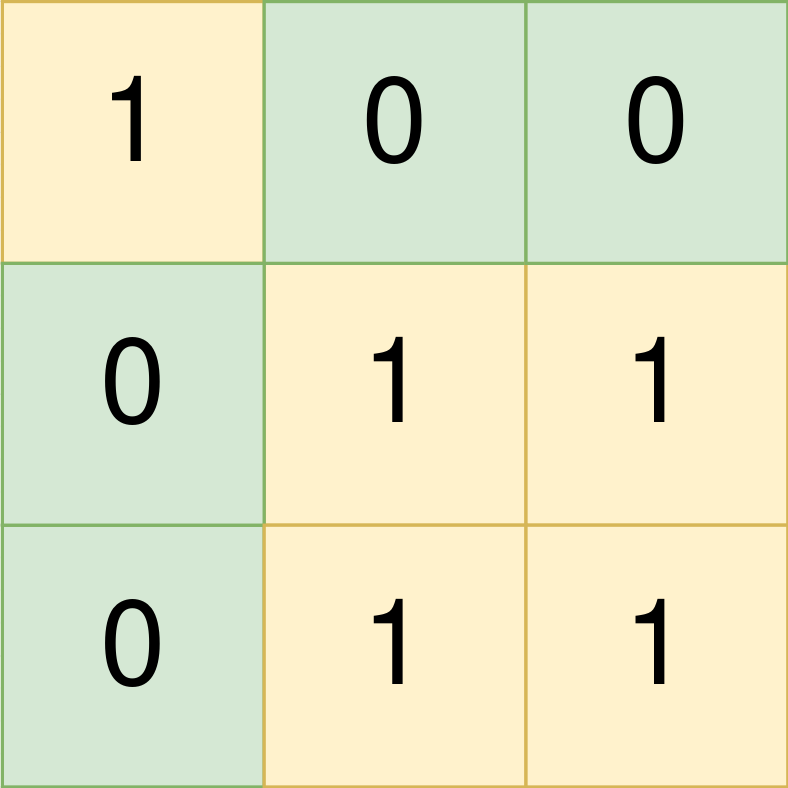
 * ![](https://assets.leetcode.com/uploads/2021/07/27/screenshot-2021-07-27-at-12-23-15-copy-of-diagram-drawio-diagrams-net.png)
 *
 * **Input:** land = \[\[1,0,0],[0,1,1],[0,1,1]]
 *
 * **Output:** [[0,0,0,0],[1,1,2,2]]
 *
 * **Explanation:**
 *
 * The first group has a top left corner at land[0][0] and a bottom right corner at land[0][0].
 *
 * The second group has a top left corner at land[1][1] and a bottom right corner at land[2][2]. 
 *
 * **Example 2:**
 *
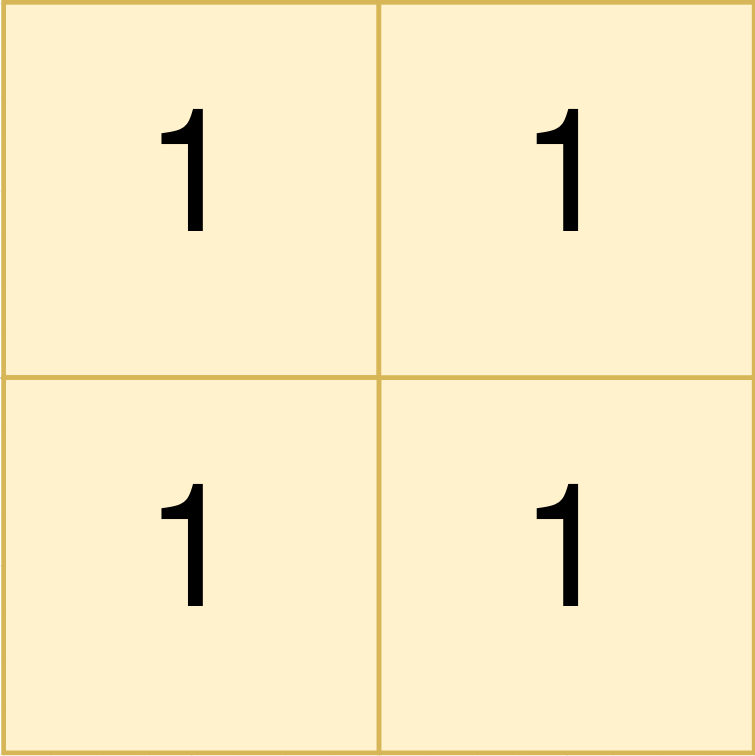
 * ![](https://assets.leetcode.com/uploads/2021/07/27/screenshot-2021-07-27-at-12-30-26-copy-of-diagram-drawio-diagrams-net.png)
 *
 * **Input:** land = \[\[1,1],[1,1]]
 *
 * **Output:** [[0,0,1,1]]
 *
 * **Explanation:**
 *
 * The first group has a top left corner at land[0][0] and a bottom right corner at land[1][1]. 
 *
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/07/27/screenshot-2021-07-27-at-12-32-24-copy-of-diagram-drawio-diagrams-net.png)
 *
 * **Input:** land = \[\[0]]
 *
 * **Output:** []
 *
 * **Explanation:** There are no groups of farmland. 
 *
 * **Constraints:**
 *
 * *   `m == land.length`
 * *   `n == land[i].length`
 * *   `1 <= m, n <= 300`
 * *   `land` consists of only `0`'s and `1`'s.
 * *   Groups of farmland are **rectangular** in shape.
**/
public class Solution {
    private final List res = new ArrayList<>();

    public int[][] findFarmland(int[][] land) {
        if (land == null || land.length == 0) {
            return new int[][] {};
        }
        int m = land.length;
        int n = land[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (land[i][j] == 1) {
                    int[] dirs = new int[4];
                    dirs[0] = i;
                    dirs[1] = j;
                    dirs[2] = i;
                    dirs[3] = j;
                    dfs(land, i, j, dirs);
                    res.add(dirs);
                }
            }
        }
        return res.toArray(new int[0][]);
    }

    private void dfs(int[][] land, int i, int j, int[] dirs) {
        if (i < 0 || i >= land.length || j < 0 || j >= land[0].length || land[i][j] != 1) {
            return;
        }
        land[i][j] = -1;
        dfs(land, i + 1, j, dirs);
        dfs(land, i, j + 1, dirs);
        dirs[0] = Math.min(dirs[0], i);
        dirs[1] = Math.min(dirs[1], j);
        dirs[2] = Math.max(dirs[2], i);
        dirs[3] = Math.max(dirs[3], j);
    }
}