g2101_2200.s2101_detonate_the_maximum_bombs.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g2101_2200.s2101_detonate_the_maximum_bombs;

// #Medium #Array #Math #Depth_First_Search #Breadth_First_Search #Graph #Geometry
// #2022_05_31_Time_27_ms_(94.17%)_Space_49.6_MB_(48.45%)

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 2101 - Detonate the Maximum Bombs\.
 *
 * Medium
 *
 * You are given a list of bombs. The **range** of a bomb is defined as the area where its effect can be felt. This area is in the shape of a **circle** with the center as the location of the bomb.
 *
 * The bombs are represented by a **0-indexed** 2D integer array `bombs` where bombs[i] = [x_i, y_i, r_i]. x_i and y_i denote the X-coordinate and Y-coordinate of the location of the i^th bomb, whereas r_i denotes the **radius** of its range.
 *
 * You may choose to detonate a **single** bomb. When a bomb is detonated, it will detonate **all bombs** that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
 *
 * Given the list of `bombs`, return _the **maximum** number of bombs that can be detonated if you are allowed to detonate **only one** bomb_.
 *
 * **Example 1:**
 *
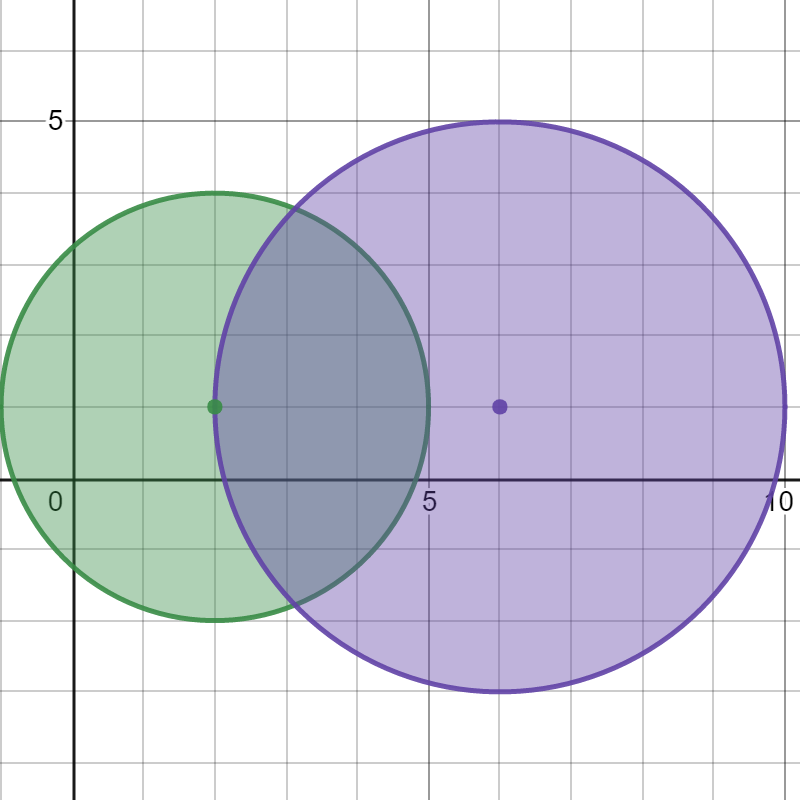
 * ![](https://assets.leetcode.com/uploads/2021/11/06/desmos-eg-3.png)
 *
 * **Input:** bombs = \[\[2,1,3],[6,1,4]]
 *
 * **Output:** 2
 *
 * **Explanation:** 
 *
 * The above figure shows the positions and ranges of the 2 bombs. 
 *
 * If we detonate the left bomb, the right bomb will not be affected. 
 *
 * But if we detonate the right bomb, both bombs will be detonated. 
 *
 * So the maximum bombs that can be detonated is max(1, 2) = 2.
 *
 * **Example 2:**
 *
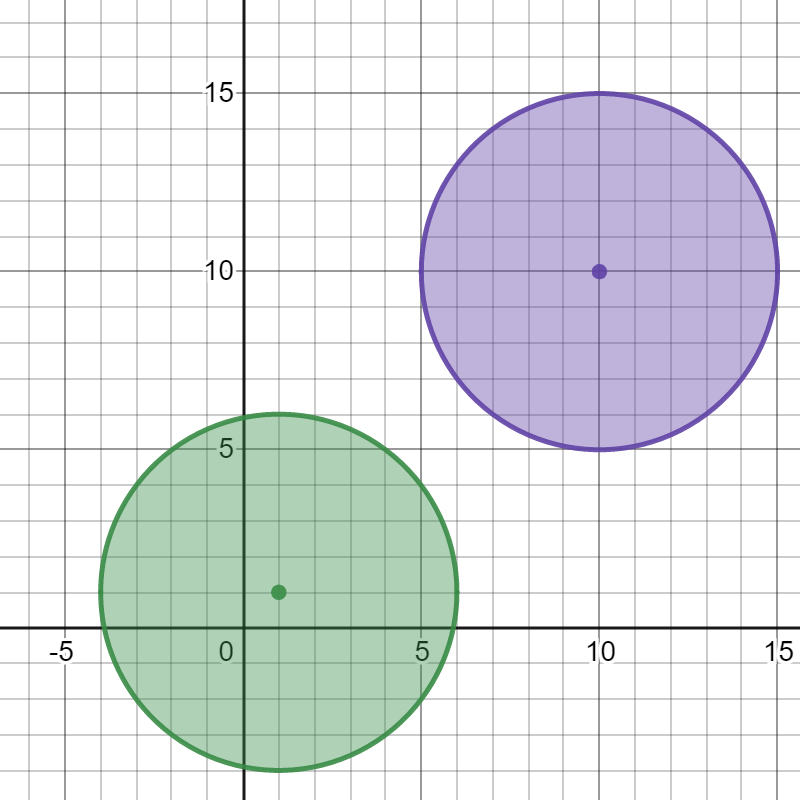
 * ![](https://assets.leetcode.com/uploads/2021/11/06/desmos-eg-2.png)
 *
 * **Input:** bombs = \[\[1,1,5],[10,10,5]]
 *
 * **Output:** 1
 *
 * **Explanation:** Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
 *
 * **Example 3:**
 *
 * ![](https://assets.leetcode.com/uploads/2021/11/07/desmos-eg1.png)
 *
 * **Input:** bombs = \[\[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
 *
 * **Output:** 5
 *
 * **Explanation:** The best bomb to detonate is bomb 0 because: 
 *
 * - Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0. 
 *
 * - Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2. 
 *
 * - Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3. 
 *   
 * Thus all 5 bombs are detonated.
 *
 * **Constraints:**
 *
 * *   `1 <= bombs.length <= 100`
 * *   `bombs[i].length == 3`
 * *   1 <= x_i, y_i, r_i <= 10⁵
**/
@SuppressWarnings("unchecked")
public class Solution {
    public int maximumDetonation(int[][] bombs) {
        int n = bombs.length;
        List[] graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                double dx = bombs[i][0] - (double) bombs[j][0];
                double dy = bombs[i][1] - (double) bombs[j][1];
                double r1 = bombs[i][2];
                double r2 = bombs[j][2];
                double dist = dx * dx + dy * dy;
                if (dist <= r1 * r1) {
                    graph[i].add(j);
                }
                if (dist <= r2 * r2) {
                    graph[j].add(i);
                }
            }
        }
        boolean[] visited = new boolean[n];
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans = Math.max(ans, dfs(graph, i, visited));
            if (ans == n) {
                return ans;
            }
            Arrays.fill(visited, false);
        }
        return ans;
    }

    private int dfs(List[] graph, int i, boolean[] visited) {
        int cc = 0;
        if (visited[i]) {
            return 0;
        }
        visited[i] = true;
        for (int neigh : graph[i]) {
            cc += dfs(graph, neigh, visited);
        }
        return cc + 1;
    }
}