g2301_2400.s2368_reachable_nodes_with_restrictions.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g2301_2400.s2368_reachable_nodes_with_restrictions;

// #Medium #Array #Hash_Table #Depth_First_Search #Breadth_First_Search #Tree #Graph
// #2022_08_16_Time_59_ms_(85.71%)_Space_89.6_MB_(85.71%)

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;

/**
 * 2368 - Reachable Nodes With Restrictions\.
 *
 * Medium
 *
 * There is an undirected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
 *
 * You are given a 2D integer array `edges` of length `n - 1` where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree. You are also given an integer array `restricted` which represents **restricted** nodes.
 *
 * Return _the **maximum** number of nodes you can reach from node_ `0` _without visiting a restricted node._
 *
 * Note that node `0` will **not** be a restricted node.
 *
 * **Example 1:**
 *
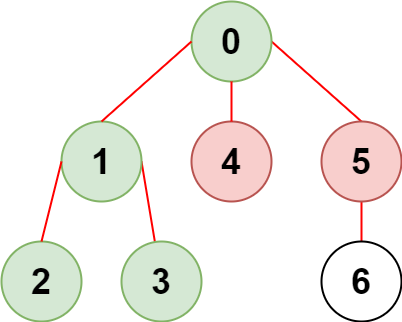
 * ![](https://assets.leetcode.com/uploads/2022/06/15/ex1drawio.png)
 *
 * **Input:** n = 7, edges = \[\[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
 *
 * **Output:** 4
 *
 * **Explanation:** The diagram above shows the tree. We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.
 *
 * **Example 2:**
 *
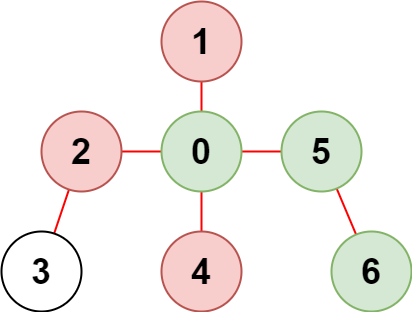
 * ![](https://assets.leetcode.com/uploads/2022/06/15/ex2drawio.png)
 *
 * **Input:** n = 7, edges = \[\[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
 *
 * **Output:** 3
 *
 * **Explanation:** The diagram above shows the tree. We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.
 *
 * **Constraints:**
 *
 * *   2 <= n <= 10⁵
 * *   `edges.length == n - 1`
 * *   `edges[i].length == 2`
 * *   0 <= a_i, b_i < n
 * *   a_i != b_i
 * *   `edges` represents a valid tree.
 * *   `1 <= restricted.length < n`
 * *   `1 <= restricted[i] < n`
 * *   All the values of `restricted` are **unique**.
**/
@SuppressWarnings("unchecked")
public class Solution {
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        List[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int src = edge[0];
            int dest = edge[1];
            graph[src].add(dest);
            graph[dest].add(src);
        }
        Queue q = new ArrayDeque<>();
        boolean[] visited = new boolean[n];
        q.offer(0);
        visited[0] = true;
        for (int node : restricted) {
            visited[node] = true;
        }
        int ans = 0;
        while (!q.isEmpty()) {
            int vertex = q.poll();
            ans++;
            for (int neighbour : graph[vertex]) {
                if (!visited[neighbour]) {
                    q.offer(neighbour);
                    visited[neighbour] = true;
                }
            }
        }
        return ans;
    }
}