g2301_2400.s2392_build_a_matrix_with_conditions.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g2301_2400.s2392_build_a_matrix_with_conditions;

// #Hard #Array #Matrix #Graph #Topological_Sort
// #2022_09_02_Time_9_ms_(97.22%)_Space_50.2_MB_(99.69%)

import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;

/**
 * 2392 - Build a Matrix With Conditions\.
 *
 * Hard
 *
 * You are given a **positive** integer `k`. You are also given:
 *
 * *   a 2D integer array `rowConditions` of size `n` where rowConditions[i] = [above_i, below_i], and
 * *   a 2D integer array `colConditions` of size `m` where colConditions[i] = [left_i, right_i].
 *
 * The two arrays contain integers from `1` to `k`.
 *
 * You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`.
 *
 * The matrix should also satisfy the following conditions:
 *
 * *   The number above_i should appear in a **row** that is strictly **above** the row at which the number below_i appears for all `i` from `0` to `n - 1`.
 * *   The number left_i should appear in a **column** that is strictly **left** of the column at which the number right_i appears for all `i` from `0` to `m - 1`.
 *
 * Return _**any** matrix that satisfies the conditions_. If no answer exists, return an empty matrix.
 *
 * **Example 1:**
 *
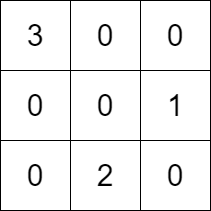
 * ![](https://assets.leetcode.com/uploads/2022/07/06/gridosdrawio.png)
 *
 * **Input:** k = 3, rowConditions = \[\[1,2],[3,2]], colConditions = \[\[2,1],[3,2]]
 *
 * **Output:** [[3,0,0],[0,0,1],[0,2,0]]
 *
 * **Explanation:** The diagram above shows a valid example of a matrix that satisfies all the conditions.
 *
 * The row conditions are the following:
 *
 * - Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
 *
 * - Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
 *
 * The column conditions are the following:
 *
 * - Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
 *
 * - Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
 *
 * Note that there may be multiple correct answers. 
 *
 * **Example 2:**
 *
 * **Input:** k = 3, rowConditions = \[\[1,2],[2,3],[3,1],[2,3]], colConditions = \[\[2,1]]
 *
 * **Output:** []
 *
 * **Explanation:** From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
 *
 * No matrix can satisfy all the conditions, so we return the empty matrix. 
 *
 * **Constraints:**
 *
 * *   `2 <= k <= 400`
 * *   1 <= rowConditions.length, colConditions.length <= 10⁴
 * *   `rowConditions[i].length == colConditions[i].length == 2`
 * *   1 <= above_i, below_i, left_i, right_i <= k
 * *   above_i != below_i
 * *   left_i != right_i
**/
public class Solution {
    // Using topological sort to solve this problem
    public int[][] buildMatrix(int k, int[][] rowC, int[][] colC) {
        // First, get the topo-sorted of row and col
        List row = toposort(k, rowC);
        List col = toposort(k, colC);
        // base case: when the length of row or col is less than k, return empty.
        // That is: there is a loop in established graph
        if (row.size() < k || col.size() < k) {
            return new int[0][0];
        }
        int[][] res = new int[k][k];
        Map map = new HashMap<>();
        for (int i = 0; i < k; i++) {
            // we record the number corresbonding to each column:
            // [number, column index]
            map.put(col.get(i), i);
        }
        // col: 3 2 1
        // row: 1 3 2
        for (int i = 0; i < k; i++) {
            // For each row: we have number row.get(i). And we need to know
            // which column we need to assign, which is from map.get(row.get(i))
            // known by map.get()
            res[i][map.get(row.get(i))] = row.get(i);
        }
        return res;
    }

    private List toposort(int k, int[][] matrix) {
        // need a int[] to record the indegree of each number [1, k]
        int[] deg = new int[k + 1];
        // need a list to record the order of each number, then return this list
        List res = new ArrayList<>();
        // need a 2-D list to be the graph, and fill the graph
        List> graph = new ArrayList<>();
        for (int i = 0; i < k; i++) {
            graph.add(new ArrayList<>());
        }
        // need a queue to do the BFS
        Queue queue = new LinkedList<>();
        // First, we need to establish the graph, following the given matrix
        for (int[] a : matrix) {
            int from = a[0];
            int to = a[1];
            graph.get(from - 1).add(to);
            deg[to]++;
        }
        // Second, after building a graph, we start the bfs,
        // that is, traverse the node with 0 degree
        for (int i = 1; i <= k; i++) {
            if (deg[i] == 0) {
                queue.offer(i);
                res.add(i);
            }
        }
        // Third, start the topo sort
        while (!queue.isEmpty()) {
            int node = queue.poll();
            List list = graph.get(node - 1);
            for (int i : list) {
                if (--deg[i] == 0) {
                    queue.offer(i);
                    res.add(i);
                }
            }
        }
        return res;
    }
}