g2301_2400.s2397_maximum_rows_covered_by_columns.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g2301_2400.s2397_maximum_rows_covered_by_columns;

// #Medium #Array #Matrix #Bit_Manipulation #Backtracking #Enumeration
// #2022_09_14_Time_1_ms_(100.00%)_Space_40.7_MB_(93.95%)

/**
 * 2397 - Maximum Rows Covered by Columns\.
 *
 * Medium
 *
 * You are given a **0-indexed** `m x n` binary matrix `matrix` and an integer `numSelect`, which denotes the number of **distinct** columns you must select from `matrix`.
 *
 * Let us consider s = {c₁, c₂, ...., c_numSelect} as the set of columns selected by you. A row `row` is **covered** by `s` if:
 *
 * *   For each cell `matrix[row][col]` (`0 <= col <= n - 1`) where `matrix[row][col] == 1`, `col` is present in `s` or,
 * *   **No cell** in `row` has a value of `1`.
 *
 * You need to choose `numSelect` columns such that the number of rows that are covered is **maximized**.
 *
 * Return _the **maximum** number of rows that can be **covered** by a set of_ `numSelect` _columns._
 *
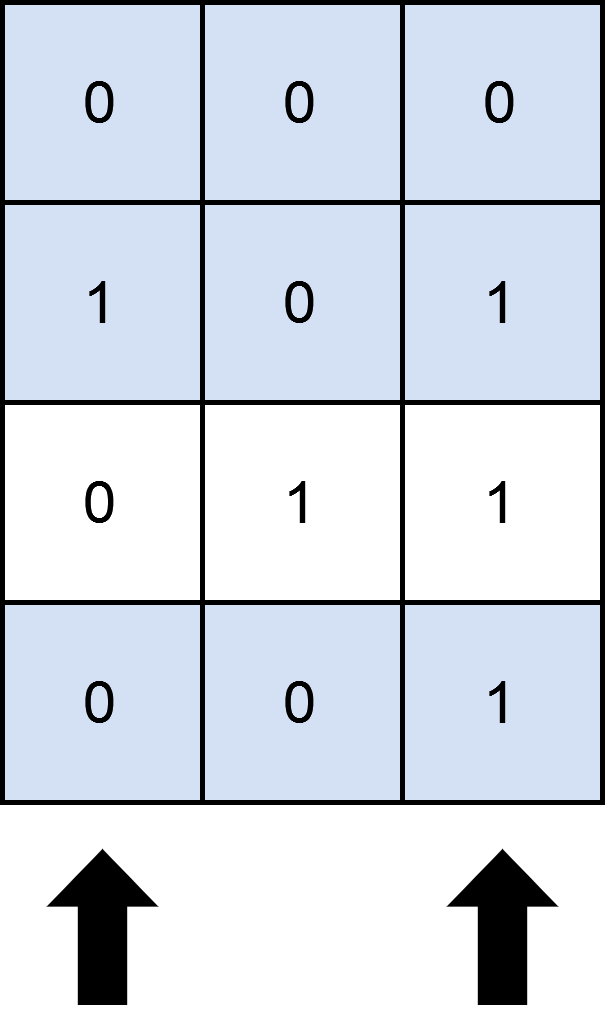
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2022/07/14/rowscovered.png)
 *
 * **Input:** matrix = \[\[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
 *
 * **Output:** 3
 *
 * **Explanation:** One possible way to cover 3 rows is shown in the diagram above.
 *
 * We choose s = {0, 2}.
 *
 * - Row 0 is covered because it has no occurrences of 1.
 *
 * - Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
 *
 * - Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
 *
 * - Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
 *
 * Thus, we can cover three rows.
 *
 * Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered. 
 *
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2022/07/14/rowscovered2.png)
 *
 * **Input:** matrix = \[\[1],[0]], numSelect = 1
 *
 * **Output:** 2
 *
 * **Explanation:** Selecting the only column will result in both rows being covered since the entire matrix is selected.
 *
 * Therefore, we return 2. 
 *
 * **Constraints:**
 *
 * *   `m == matrix.length`
 * *   `n == matrix[i].length`
 * *   `1 <= m, n <= 12`
 * *   `matrix[i][j]` is either `0` or `1`.
 * *   `1 <= numSelect <= n`
**/
public class Solution {
    private int ans = 0;

    public int maximumRows(int[][] matrix, int numSelect) {
        dfs(matrix, /*colIndex=*/ 0, numSelect, /*mask=*/ 0);
        return ans;
    }

    private void dfs(int[][] matrix, int colIndex, int leftColsCount, int mask) {
        if (leftColsCount == 0) {
            ans = Math.max(ans, getAllZerosRowCount(matrix, mask));
            return;
        }
        if (colIndex == matrix[0].length) {
            return;
        }
        // choose this column
        dfs(matrix, colIndex + 1, leftColsCount - 1, mask | 1 << colIndex);
        // not choose this column
        dfs(matrix, colIndex + 1, leftColsCount, mask);
    }

    private int getAllZerosRowCount(int[][] matrix, int mask) {
        int count = 0;
        for (int[] row : matrix) {
            boolean isAllZeros = true;
            for (int i = 0; i < row.length; ++i) {
                if (row[i] == 1 && (mask >> i & 1) == 0) {
                    isAllZeros = false;
                    break;
                }
            }
            if (isAllZeros) {
                ++count;
            }
        }
        return count;
    }
}