
g2401_2500.s2463_minimum_total_distance_traveled.Solution Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
package g2401_2500.s2463_minimum_total_distance_traveled;
// #Hard #Array #Dynamic_Programming #Sorting #2023_01_07_Time_2_ms_(100.00%)_Space_40.3_MB_(98.21%)
import java.util.Arrays;
import java.util.List;
/**
* 2463 - Minimum Total Distance Traveled\.
*
* Hard
*
* There are some robots and factories on the X-axis. You are given an integer array `robot` where `robot[i]` is the position of the ith robot. You are also given a 2D integer array `factory` where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.
*
* The positions of each robot are **unique**. The positions of each factory are also **unique**. Note that a robot can be **in the same position** as a factory initially.
*
* All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.
*
* **At any moment** , you can set the initial direction of moving for **some** robot. Your target is to minimize the total distance traveled by all the robots.
*
* Return _the minimum total distance traveled by all the robots_. The test cases are generated such that all the robots can be repaired.
*
* **Note that**
*
* * All robots move at the same speed.
* * If two robots move in the same direction, they will never collide.
* * If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
* * If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
* * If the robot moved from a position `x` to a position `y`, the distance it moved is `|y - x|`.
*
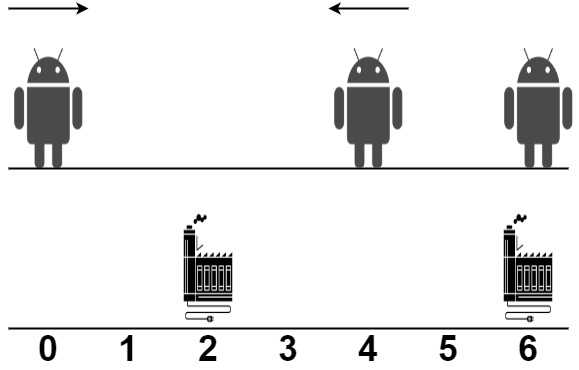
* **Example 1:**
*
* 
*
* **Input:** robot = [0,4,6], factory = \[\[2,2],[6,2]]
*
* **Output:** 4
*
* **Explanation:** As shown in the figure:
*
* - The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
*
* - The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
*
* - The third robot at position 6 will be repaired at the second factory. It does not need to move.
*
* The limit of the first factory is 2, and it fixed 2 robots.
*
* The limit of the second factory is 2, and it fixed 1 robot.
*
* The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.
*
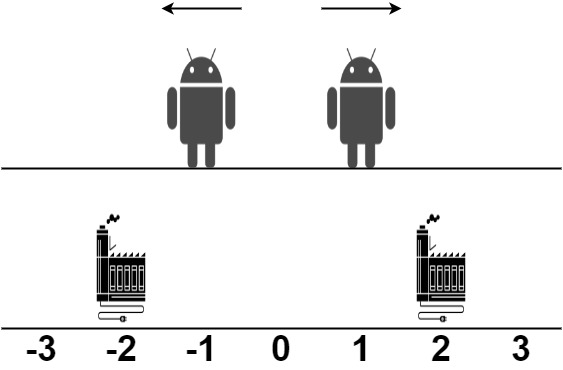
* **Example 2:**
*
* 
*
* **Input:** robot = [1,-1], factory = \[\[-2,1],[2,1]]
*
* **Output:** 2
*
* **Explanation:** As shown in the figure:
*
* - The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
*
* - The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
*
* The limit of the first factory is 1, and it fixed 1 robot. The limit of the second factory is 1, and it fixed 1 robot.
*
* The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.
*
* **Constraints:**
*
* * `1 <= robot.length, factory.length <= 100`
* * `factory[j].length == 2`
* * -109 <= robot[i], positionj <= 109
* * 0 <= limitj <= robot.length
* * The input will be generated such that it is always possible to repair every robot.
**/
@SuppressWarnings("java:S3358")
public class Solution {
public long minimumTotalDistance(List robot, int[][] f) {
// sort factories :
// 1. move all factories with 0-capacity to the end
// 2. sort everything else by x-position in asc order
Arrays.sort(f, (a, b) -> (a[1] == 0) ? 1 : (b[1] == 0) ? -1 : a[0] - b[0]);
// Sort robots by x-position in asc order
// As we don't know the implementation of the List that is passed, it is better to map it to
// an array explicitly
int[] r = new int[robot.size()];
int i = 0;
for (int x : robot) {
r[i++] = x;
}
Arrays.sort(r);
// An array to be used for tracking robots assigned to each factory
int[][] d = new int[f.length][2];
// For each robot starting from the rightmost find the most optimal destination factory
// and add it's cost to the result.
long res = 0;
for (i = r.length - 1; i >= 0; i--) {
res += pop(d, i, r, f);
}
return res;
}
private long pop(int[][] d, int i, int[] r, int[][] f) {
long cost = Long.MAX_VALUE;
int j;
// try assigning robot to each factory starting from the leftmost
for (j = 0; j < d.length; j++) {
// cost of adding robot to the current factory
long t = Math.abs(r[i] - f[j][0]);
int tj = j;
// if current factory is full calculate the cost of moving the rightmost robot in the
// factory to the next one
// and add the calculated cost to the current cost.
// repeat the same action until we fit our robots to factories.
while (tj < d.length && d[tj][1] == f[tj][1]) {
// if we faced a factory with 0-capactity or the rightmost factory
// it would mean we reached the end and cannot fit our robot to the current factory
if (d[tj][1] == 0 || tj == d.length - 1) {
t = Long.MAX_VALUE;
break;
}
int l = d[tj][0] + d[tj][1] - 1;
t += Math.abs(f[tj + 1][0] - r[l]) - Math.abs(f[tj][0] - r[l]);
++tj;
}
// if the cost for adding robot to the current factory is greater than the previous one
// it means that the previous one was the most optimal
if (t > cost) {
break;
}
cost = t;
}
// assign current robot to the previous factory and move any non-fit robots to the right
d[j - 1][0] = i;
int tj = j - 1;
while (d[tj][1] == f[tj][1]) {
d[tj + 1][0] = d[tj][0] + d[tj][1];
++tj;
}
d[tj][1]++;
return cost;
}
}
© 2015 - 2025 Weber Informatics LLC | Privacy Policy