g2401_2500.s2498_frog_jump_ii.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g2401_2500.s2498_frog_jump_ii;

// #Medium #Array #Greedy #Binary_Search #2023_02_12_Time_1_ms_(100.00%)_Space_55.8_MB_(66.50%)

/**
 * 2498 - Frog Jump II\.
 *
 * Medium
 *
 * You are given a **0-indexed** integer array `stones` sorted in **strictly increasing order** representing the positions of stones in a river.
 *
 * A frog, initially on the first stone, wants to travel to the last stone and then return to the first stone. However, it can jump to any stone **at most once**.
 *
 * The **length** of a jump is the absolute difference between the position of the stone the frog is currently on and the position of the stone to which the frog jumps.
 *
 * *   More formally, if the frog is at `stones[i]` and is jumping to `stones[j]`, the length of the jump is `|stones[i] - stones[j]|`.
 *
 * The **cost** of a path is the **maximum length of a jump** among all jumps in the path.
 *
 * Return _the **minimum** cost of a path for the frog_.
 *
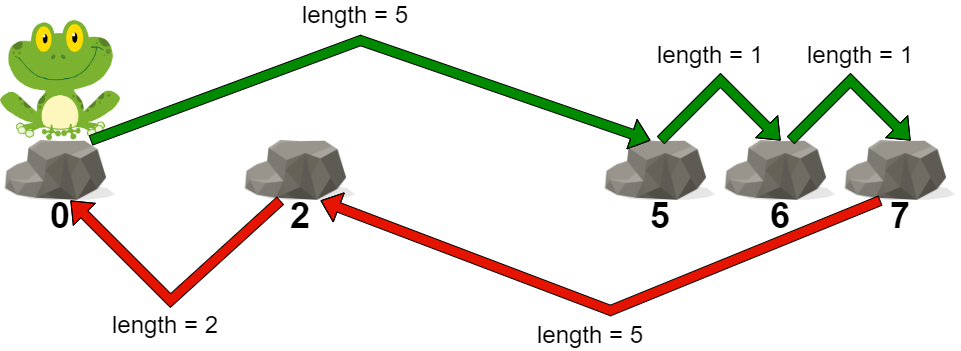
 * **Example 1:**
 *
 * ![](https://assets.leetcode.com/uploads/2022/11/14/example-1.png)
 *
 * **Input:** stones = [0,2,5,6,7]
 *
 * **Output:** 5
 *
 * **Explanation:** The above figure represents one of the optimal paths the frog can take.
 *
 * The cost of this path is 5, which is the maximum length of a jump.
 *
 * Since it is not possible to achieve a cost of less than 5, we return it. 
 *
 * **Example 2:**
 *
 * ![](https://assets.leetcode.com/uploads/2022/11/14/example-2.png)
 *
 * **Input:** stones = [0,3,9]
 *
 * **Output:** 9
 *
 * **Explanation:** The frog can jump directly to the last stone and come back to the first stone.
 *
 * In this case, the length of each jump will be 9. The cost for the path will be max(9, 9) = 9.
 *
 * It can be shown that this is the minimum achievable cost. 
 *
 * **Constraints:**
 *
 * *   2 <= stones.length <= 10⁵
 * *   0 <= stones[i] <= 10⁹
 * *   `stones[0] == 0`
 * *   `stones` is sorted in a strictly increasing order.
**/
public class Solution {
    public int maxJump(int[] stones) {
        int n = stones.length;
        int max = 0;
        for (int i = 2; i < n; i++) {
            int gap = stones[i] - stones[i - 2];
            if (gap > max) {
                max = gap;
            }
        }
        if (n > 2) {
            return max;
        } else {
            return stones[1] - stones[0];
        }
    }
}