
g2601_2700.s2603_collect_coins_in_a_tree.Solution Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
package g2601_2700.s2603_collect_coins_in_a_tree;
// #Hard #Array #Tree #Graph #Topological_Sort
// #2023_08_29_Time_26_ms_(100.00%)_Space_66.3_MB_(32.97%)
import java.util.ArrayList;
import java.util.List;
/**
* 2603 - Collect Coins in a Tree\.
*
* Hard
*
* There exists an undirected and unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given an integer `n` and a 2D integer array edges of length `n - 1`, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an array `coins` of size `n` where `coins[i]` can be either `0` or `1`, where `1` indicates the presence of a coin in the vertex `i`.
*
* Initially, you choose to start at any vertex in the tree. Then, you can perform the following operations any number of times:
*
* * Collect all the coins that are at a distance of at most `2` from the current vertex, or
* * Move to any adjacent vertex in the tree.
*
* Find _the minimum number of edges you need to go through to collect all the coins and go back to the initial vertex_.
*
* Note that if you pass an edge several times, you need to count it into the answer several times.
*
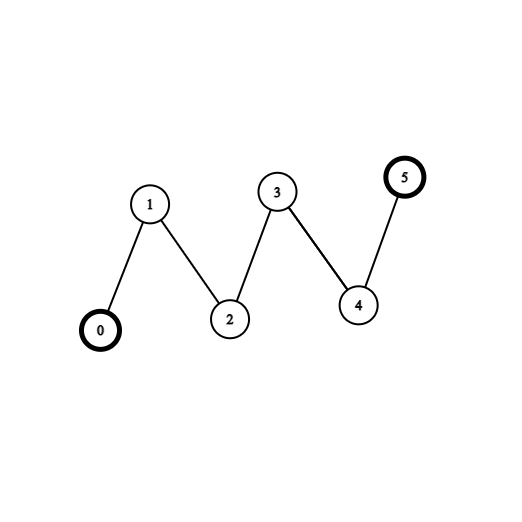
* **Example 1:**
*
* 
*
* **Input:** coins = [1,0,0,0,0,1], edges = \[\[0,1],[1,2],[2,3],[3,4],[4,5]]
*
* **Output:** 2
*
* **Explanation:** Start at vertex 2, collect the coin at vertex 0, move to vertex 3, collect the coin at vertex 5 then move back to vertex 2.
*
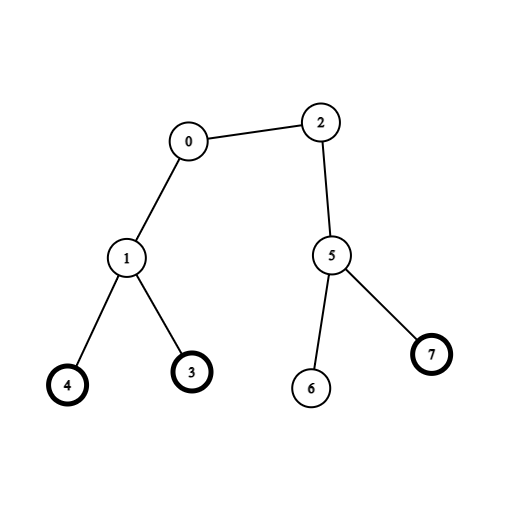
* **Example 2:**
*
* 
*
* **Input:** coins = [0,0,0,1,1,0,0,1], edges = \[\[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
*
* **Output:** 2
*
* **Explanation:** Start at vertex 0, collect the coins at vertices 4 and 3, move to vertex 2, collect the coin at vertex 7, then move back to vertex 0.
*
* **Constraints:**
*
* * `n == coins.length`
* * 1 <= n <= 3 * 104
* * `0 <= coins[i] <= 1`
* * `edges.length == n - 1`
* * `edges[i].length == 2`
* * 0 <= ai, bi < n
* * ai != bi
* * `edges` represents a valid tree.
**/
@SuppressWarnings("unchecked")
public class Solution {
private int[] coins;
private List[] graph;
private int sum;
private int ret;
public int collectTheCoins(int[] coins, int[][] edges) {
int n = coins.length;
this.coins = coins;
graph = new ArrayList[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] edge : edges) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
for (int coin : coins) {
sum += coin;
}
dfs(0, -1);
return Math.max(2 * (ret - 1), 0);
}
private int dfs(int node, int pre) {
int cnt = 0;
int s = 0;
for (int nn : graph[node]) {
if (nn != pre) {
int r = dfs(nn, node);
if (r - coins[nn] > 0) {
cnt++;
}
s += r;
}
}
if (pre != -1 && sum - s - coins[node] - coins[pre] > 0) {
cnt++;
}
if (cnt >= 2) {
ret++;
}
return s + coins[node];
}
}