g2601_2700.s2614_prime_in_diagonal.Solution Maven / Gradle / Ivy

Go to download

Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation

Java-based LeetCode algorithm problem solutions, regularly updated

There is a newer version: 1.38

package g2601_2700.s2614_prime_in_diagonal;

// #Easy #Array #Math #Matrix #Number_Theory #2023_08_30_Time_0_ms_(100.00%)_Space_56.5_MB_(21.81%)

/**
 * 2614 - Prime In Diagonal\.
 *
 * Easy
 *
 * You are given a 0-indexed two-dimensional integer array `nums`.
 *
 * Return _the largest **prime** number that lies on at least one of the **diagonals** of_ `nums`. In case, no prime is present on any of the diagonals, return _0._
 *
 * Note that:
 *
 * *   An integer is **prime** if it is greater than `1` and has no positive integer divisors other than `1` and itself.
 * *   An integer `val` is on one of the **diagonals** of `nums` if there exists an integer `i` for which `nums[i][i] = val` or an `i` for which `nums[i][nums.length - i - 1] = val`.
 *
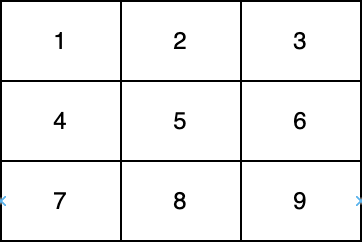
 * ![](https://assets.leetcode.com/uploads/2023/03/06/screenshot-2023-03-06-at-45648-pm.png)
 *
 * In the above diagram, one diagonal is **[1,5,9]** and another diagonal is **[3,5,7]**.
 *
 * **Example 1:**
 *
 * **Input:** nums = \[\[1,2,3],[5,6,7],[9,10,11]]
 *
 * **Output:** 11
 *
 * **Explanation:** The numbers 1, 3, 6, 9, and 11 are the only numbers present on at least one of the diagonals. Since 11 is the largest prime, we return 11.
 *
 * **Example 2:**
 *
 * **Input:** nums = \[\[1,2,3],[5,17,7],[9,11,10]]
 *
 * **Output:** 17
 *
 * **Explanation:** The numbers 1, 3, 9, 10, and 17 are all present on at least one of the diagonals. 17 is the largest prime, so we return 17.
 *
 * **Constraints:**
 *
 * *   `1 <= nums.length <= 300`
 * *   nums.length == nums_i.length
 * *   1 <= nums[i][j] <= 4*10⁶
**/
public class Solution {
    public int diagonalPrime(int[][] nums) {
        int i = 0;
        int j = nums[0].length - 1;
        int lp = 0;
        while (i < nums.length) {
            int n1 = nums[i][i];
            if (n1 > lp && isPrime(n1)) {
                lp = n1;
            }
            int n2 = nums[i][j];
            if (n2 > lp && isPrime(n2)) {
                lp = n2;
            }
            i++;
            j--;
        }
        return lp;
    }

    private boolean isPrime(int n) {
        if (n == 1) {
            return false;
        }
        if (n == 2 || n == 3) {
            return true;
        }
        int i = 2;
        while (i <= Math.sqrt(n)) {
            if (n % i == 0) {
                return false;
            }
            i++;
        }
        return true;
    }
}