g2601_2700.s2699_modify_graph_edge_weights.Solution Maven / Gradle / Ivy

Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
There is a newer version: 1.38
package g2601_2700.s2699_modify_graph_edge_weights;

// #Hard #Heap_Priority_Queue #Graph #Shortest_Path
// #2023_09_14_Time_88_ms_(85.25%)_Space_49.9_MB_(85.25%)

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;

/**
 * 2699 - Modify Graph Edge Weights\.
 *
 * Hard
 *
 * You are given an **undirected weighted** **connected** graph containing `n` nodes labeled from `0` to `n - 1`, and an integer array `edges` where edges[i] = [a_i, b_i, w_i] indicates that there is an edge between nodes a_i and b_i with weight w_i.
 *
 * Some edges have a weight of `-1` (w_i = -1), while others have a **positive** weight (w_i > 0).
 *
 * Your task is to modify **all edges** with a weight of `-1` by assigning them **positive integer values** in the range [1, 2 * 10⁹] so that the **shortest distance** between the nodes `source` and `destination` becomes equal to an integer `target`. If there are **multiple** **modifications** that make the shortest distance between `source` and `destination` equal to `target`, any of them will be considered correct.
 *
 * Return _an array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from_ `source` _to_ `destination` _equal to_ `target`_, or an **empty array** if it's impossible._
 *
 * **Note:** You are not allowed to modify the weights of edges with initial positive weights.
 *
 * **Example 1:**
 *
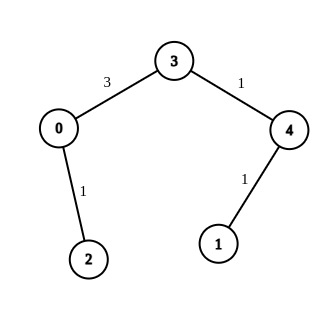 * **![](https://assets.leetcode.com/uploads/2023/04/18/graph.png)**
 *
 * **Input:** n = 5, edges = \[\[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
 *
 * **Output:** [[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
 *
 * **Explanation:** The graph above shows a possible modification to the edges, making the distance from 0 to 1 equal to 5.
 *
 * **Example 2:**
 *
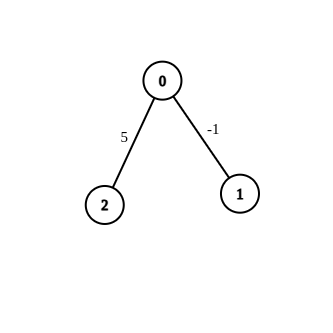 * **![](https://assets.leetcode.com/uploads/2023/04/18/graph-2.png)**
 *
 * **Input:** n = 3, edges = \[\[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
 *
 * **Output:** []
 *
 * **Explanation:** The graph above contains the initial edges. It is not possible to make the distance from 0 to 2 equal to 6 by modifying the edge with weight -1. So, an empty array is returned.
 *
 * **Example 3:**
 *
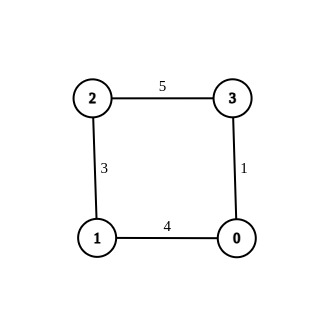 * **![](https://assets.leetcode.com/uploads/2023/04/19/graph-3.png)**
 *
 * **Input:** n = 4, edges = \[\[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
 *
 * **Output:** [[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
 *
 * **Explanation:** The graph above shows a modified graph having the shortest distance from 0 to 2 as 6.
 *
 * **Constraints:**
 *
 * *   `1 <= n <= 100`
 * *   `1 <= edges.length <= n * (n - 1) / 2`
 * *   `edges[i].length == 3`
 * *   0 <= a_i, b_i< n
 * *   w_i = -1 or 1 <= w_i<= 10⁷
 * *   a_i!= b_i
 * *   `0 <= source, destination < n`
 * *   `source != destination`
 * *   1 <= target <= 10⁹
 * *   The graph is connected, and there are no self-loops or repeated edges
**/
@SuppressWarnings({"unchecked", "java:S135"})
public class Solution {
    public int[][] modifiedGraphEdges(
            int n, int[][] edges, int source, int destination, int target) {
        List[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int i = 0; i < edges.length; i++) {
            int[] e = edges[i];
            graph[e[0]].add(new int[] {e[1], i});
            graph[e[1]].add(new int[] {e[0], i});
        }
        PriorityQueue pq = new PriorityQueue<>(Comparator.comparingInt(v -> v[1]));
        pq.add(new int[] {destination, 0});
        Integer[] distances = new Integer[n];
        processQueue(edges, source, pq, distances, graph);
        if (distances[source] > target) {
            return new int[][] {};
        }
        pq = new PriorityQueue<>(Comparator.comparingInt(v -> v[1]));
        if (distances[source] != target) {
            pq.add(new int[] {source, 0});
        }
        boolean[] visited = new boolean[n];
        while (!pq.isEmpty()) {
            int[] c = pq.poll();
            if (visited[c[0]]) {
                continue;
            }
            visited[c[0]] = true;
            if (c[0] == destination) {
                return new int[][] {};
            }
            for (int[] e : graph[c[0]]) {
                if (visited[e[0]] || distances[e[0]] == null) {
                    continue;
                }
                int dif = target - c[1] - distances[e[0]];
                if (Math.abs(edges[e[1]][2]) >= dif) {
                    continue;
                }
                if (edges[e[1]][2] == -1) {
                    edges[e[1]][2] = dif;
                    continue;
                }
                pq.add(new int[] {e[0], c[1] + edges[e[1]][2]});
            }
        }
        for (int[] e : edges) {
            if (e[2] == -1) {
                e[2] = 1;
            }
        }
        return edges;
    }

    private void processQueue(
            int[][] edges,
            int source,
            PriorityQueue pq,
            Integer[] distances,
            List[] graph) {
        while (!pq.isEmpty()) {
            int[] c = pq.poll();
            if (distances[c[0]] != null) {
                continue;
            }
            distances[c[0]] = c[1];
            if (c[0] == source) {
                continue;
            }
            for (int[] e : graph[c[0]]) {
                if (distances[e[0]] != null) {
                    continue;
                }
                pq.add(new int[] {e[0], c[1] + Math.abs(edges[e[1]][2])});
            }
        }
    }
}