g0001_0100.s0079_word_search.readme.md Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
79\. Word Search
Medium
Given an `m x n` grid of characters `board` and a string `word`, return `true` _if_ `word` _exists in the grid_.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
**Example 1:**
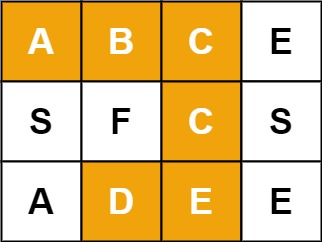
**Input:** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
**Output:** true
**Example 2:**
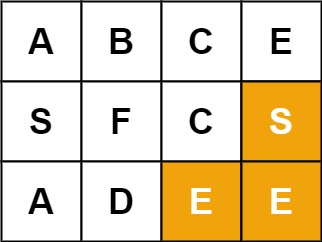
**Input:** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
**Output:** true
**Example 3:**

**Input:** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
**Output:** false
**Constraints:**
* `m == board.length`
* `n = board[i].length`
* `1 <= m, n <= 6`
* `1 <= word.length <= 15`
* `board` and `word` consists of only lowercase and uppercase English letters.
**Follow up:** Could you use search pruning to make your solution faster with a larger `board`?
To solve the "Word Search" problem in Java with the Solution class, follow these steps:
1. Define a method `exist` in the `Solution` class that takes a 2D character array `board` and a string `word` as input and returns `true` if the `word` exists in the `board`.
2. Implement a backtracking algorithm to search for the `word` in the `board`.
3. Iterate through each cell in the `board`:
- For each cell, call a recursive helper function `search` to check if the `word` can be found starting from that cell.
- If `search` returns `true`, return `true` immediately.
4. Define the `search` method to perform the recursive backtracking:
- Check if the current cell is out of bounds or if the current character in the `board` does not match the corresponding character in the `word`.
- If any of the conditions are met, return `false`.
- Mark the current cell as visited by changing its value to a special character (e.g., `#`) to avoid revisiting it.
- Recursively call `search` on neighboring cells (up, down, left, right) with the next character in the `word`.
- After exploring all possible paths from the current cell, backtrack by restoring the original value of the current cell.
5. If the `search` method reaches the end of the `word`, return `true`.
6. If no match is found after exploring all cells, return `false`.
Here's the implementation of the `exist` method in Java:
```java
class Solution {
public boolean exist(char[][] board, String word) {
int m = board.length;
int n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (search(board, word, i, j, 0))
return true;
}
}
return false;
}
private boolean search(char[][] board, String word, int i, int j, int index) {
if (index == word.length())
return true;
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != word.charAt(index))
return false;
char temp = board[i][j];
board[i][j] = '#'; // Mark as visited
boolean found = search(board, word, i + 1, j, index + 1) ||
search(board, word, i - 1, j, index + 1) ||
search(board, word, i, j + 1, index + 1) ||
search(board, word, i, j - 1, index + 1);
board[i][j] = temp; // Restore original value
return found;
}
}
```
This implementation uses backtracking to search for the word in the board, with a time complexity of O(M * N * 4^L), where M and N are the dimensions of the board and L is the length of the word.