g2301_2400.s2397_maximum_rows_covered_by_columns.readme.md Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-java21 Show documentation
Show all versions of leetcode-in-java21 Show documentation
Java-based LeetCode algorithm problem solutions, regularly updated
2397\. Maximum Rows Covered by Columns
Medium
You are given a **0-indexed** `m x n` binary matrix `matrix` and an integer `numSelect`, which denotes the number of **distinct** columns you must select from `matrix`.
Let us consider s = {c1, c2, ...., cnumSelect} as the set of columns selected by you. A row `row` is **covered** by `s` if:
* For each cell `matrix[row][col]` (`0 <= col <= n - 1`) where `matrix[row][col] == 1`, `col` is present in `s` or,
* **No cell** in `row` has a value of `1`.
You need to choose `numSelect` columns such that the number of rows that are covered is **maximized**.
Return _the **maximum** number of rows that can be **covered** by a set of_ `numSelect` _columns._
**Example 1:**
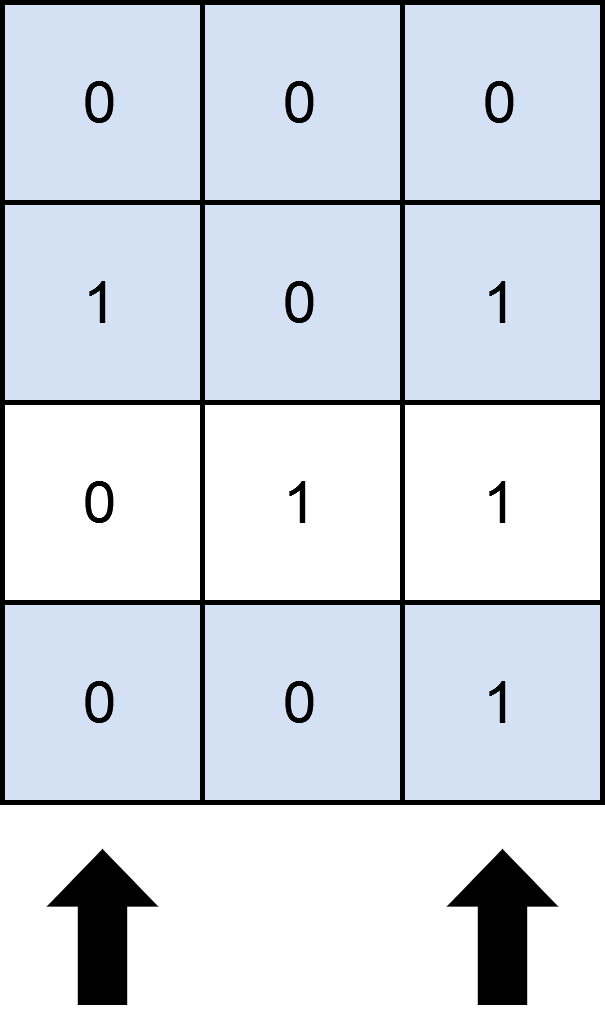
**Input:** matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
**Output:** 3
**Explanation:** One possible way to cover 3 rows is shown in the diagram above.
We choose s = {0, 2}.
- Row 0 is covered because it has no occurrences of 1.
- Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
- Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
- Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
Thus, we can cover three rows.
Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.
**Example 2:**
**Input:** matrix = [[1],[0]], numSelect = 1
**Output:** 2
**Explanation:** Selecting the only column will result in both rows being covered since the entire matrix is selected.
Therefore, we return 2.
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 12`
* `matrix[i][j]` is either `0` or `1`.
* `1 <= numSelect <= n`